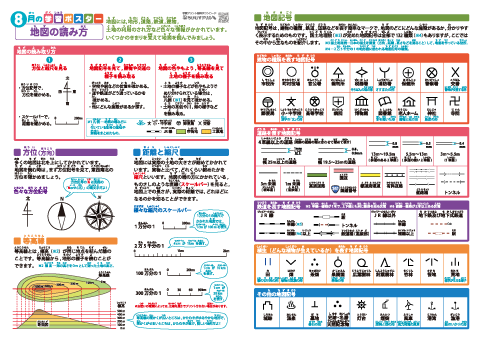
小学社会 地図の読み方 方位 距離と縮尺 等高線 地図記号 建物 道路 鉄道 植生 その他 学習ポスター クイズテスト やってみよう 無料ダウンロード ちびむすドリル 小学生学習ポスター テスト 家庭学習シート 3ステップ学習
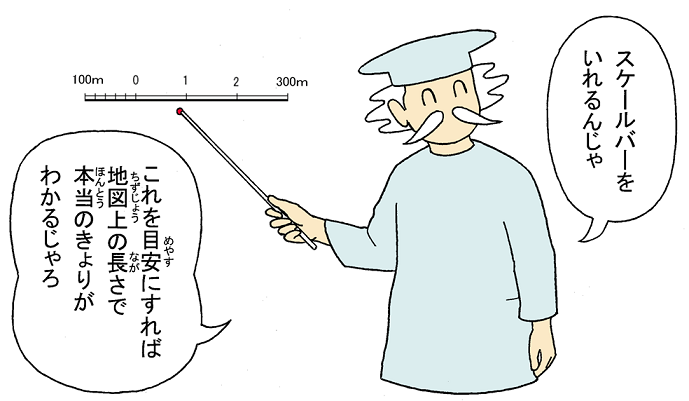
OpenStreetMap is a map of the world, created by people like you and free to use under an open license Hosting is supported by UCL, Fastly, Bytemark Hosting, and other partners縮尺は、1万分の1、25万分の1、5万分の1の3種類です。 縮尺とは、実物をどれほど縮めているかで、より縮めていれば「縮尺が小さい」、あまり縮めていなければ「縮尺が大きい」と表現します。 従って、25万分の1の方は、5万分の1より「縮尺が大きい」と言えます。 「25万分の1=」「5万分の1=」と考えると、縮尺が「大きい」「小さい」はわかり
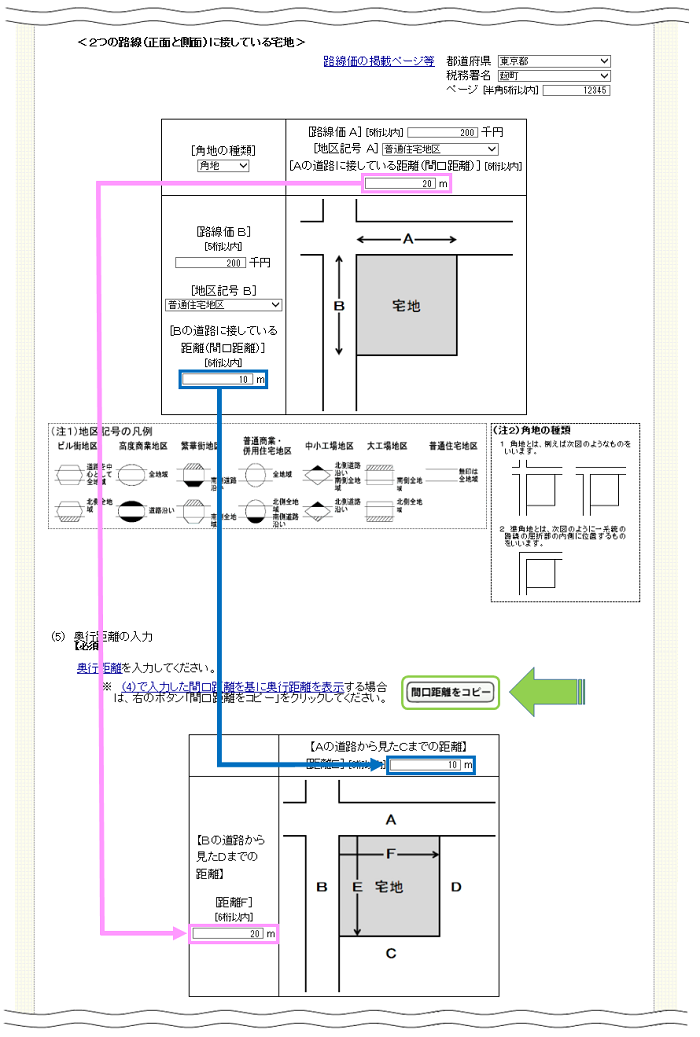
距離 記号
距離 記号-『距離』には3種類あり、 光波からターゲットまでの直接距離(斜距離 SD = Slope Distance) 斜距離を平面上に落とした時の距離(水平距離 HD = Horizontal Distance)の距離(AB)を測量する。 a=96°45′35″ AB=m B=246°4′2″ 内角=113°55′58″ bc=95m 点Bに測角儀を移して、前点(A)から次点(C)までの角度 と、次点までの距離(BC)を測量する。 2 3 cの内角=80°16′15″ dの内角=153°1′25″ eの内角=93°1′55″

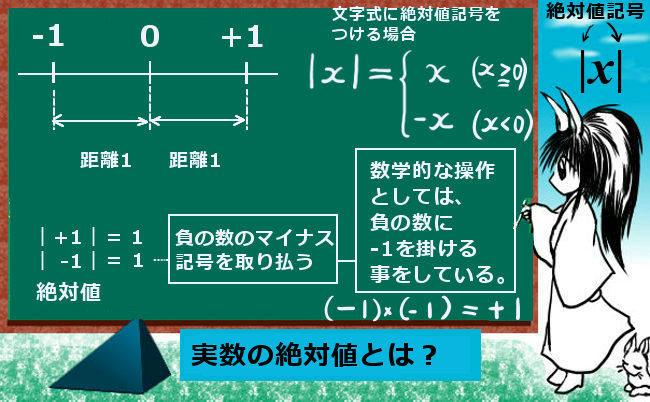
数i絶対値記号を含む方程式 不等式です Clearnote
2点間の距離を求める手順 それぞれの 座標から、ヨコの長さを求める。 それぞれの 座標から、タテの長さを求める。 ①②を用いて三平方の定理に当てはめて計算する。 完成! ちょっと、手順が多くてめんどうだなぁ と感じた方は次の公式を覚えて天文単位距離ともいう。天文学において太陽系内の天体間の距離を表わすのに用いられる長さの単位。国際的に統一された単位記号はなく,英語で au ,フランス語で ua ,ドイツ語で ae などと書かれる。量 量記号 単位の名称 単位記号 量 量記号 単位の名称 単位記号 平面角,角度 α,β,γ,θ,왃 など ラジアン rad 度 ° 分 ′ 秒 ″ 立体角 Ω ステラジアン sr 長 さ , メートル m 幅 オングストローム Å 高 さ 海里 nmile 厚 さ ,δ 天文単位 AU 半 径
とりあえず文字を使いたいときに一つ目の記号として使う,方程式の解,アルファ線 β, B \beta,\B β, B :ベータ 二つ目の記号として使う,方程式の解,ベータ線, ベータ関数 γ, Γ \gamma,\\Gamma γ, Γ :ガンマ 三つ目の記号として使う,比熱比, オイラー定数 ,ガンマ線, ガンマ関数 ,円 δ, Δ \delta,\\Delta δ, Δ :デルタ記号要素について 洋裁型紙に入れるさまざまな記号です。記号を入れることで、型紙の意図や布の処理方法を示すことができます。 記号要素の種類 10個の種類があります。 合印 長い縫い代の2つの布を縫い合わせるときに、途中につける印です。縮尺記号は、マップ上に表示されている距離とフィーチャのサイズを視覚的に示します。 縮尺記号は、複数の部分に分割されたラインまたはバーであり、 通常は 10 キロメートルや 100 マイルなどのマップ単位の倍数で長さのラベルが付いています。
距離 記号のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
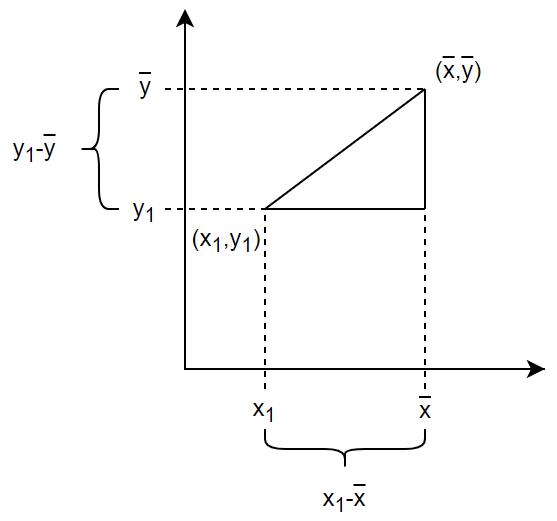 |  |  |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 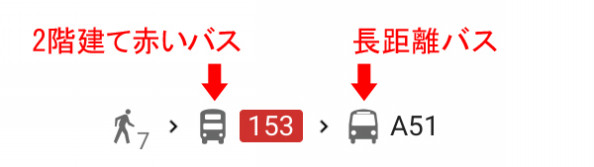 |  |
 | 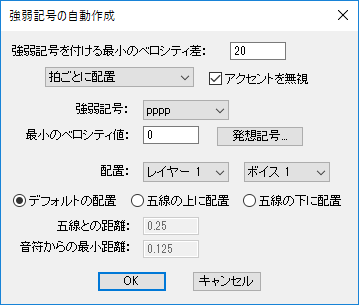 | |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | 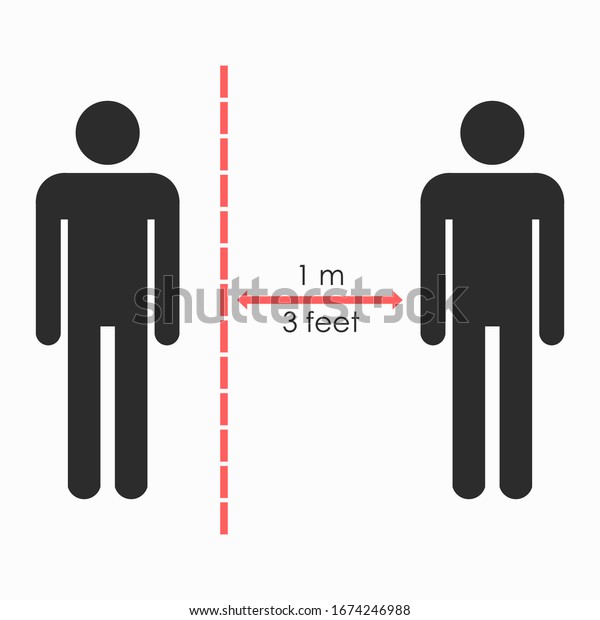 | |
「距離 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 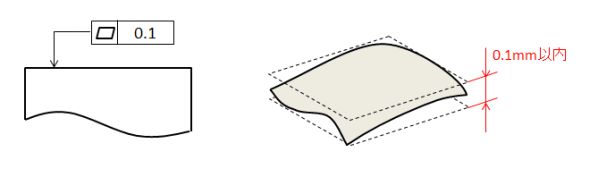 |
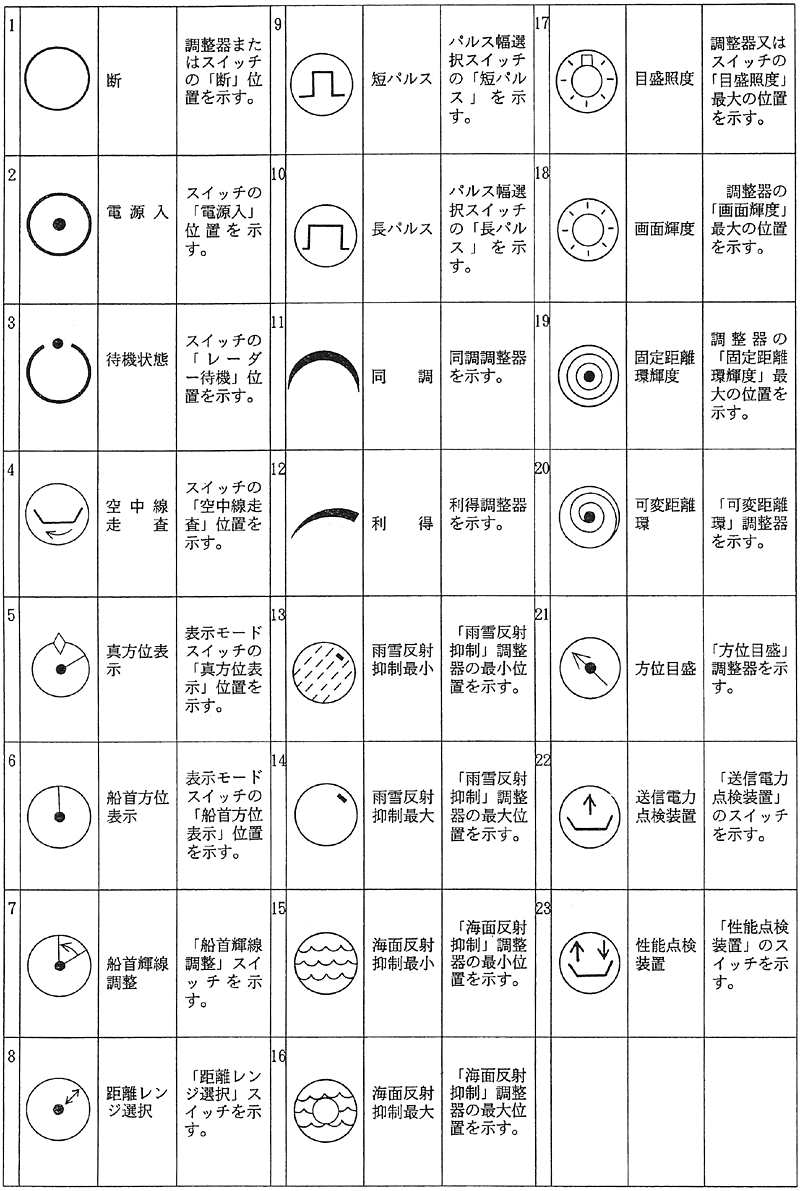
幾何公差特性の分類と記号 以下は幾何公差の記号です。 「適応形体」の「単独形体」とは、データムに関連しない(基準のデータム指示が不要)な形体です。 「 データム 」とは姿勢や位置・振れを決めるために設定した理論的で理想的な形体です。 また、「関連形体」とはデータムに関連する形体で、姿勢や位置、振れの公差を指定する形体です。 適用形体:軸間距離(mm) :大プーリピッチ円直径(mm) dp:小プーリピッチ円直径(mm) c B=Lp-157(Dp+dp) Lp :軸間距離(mm) :ピッチ周長さ(mm) Dp dp :大プーリピッチ円直径(mm) :小プーリピッチ円直径(mm) Zm Z1 θ1 :小プーリかみ合い歯数 :小プーリ歯数





0 件のコメント:
コメントを投稿