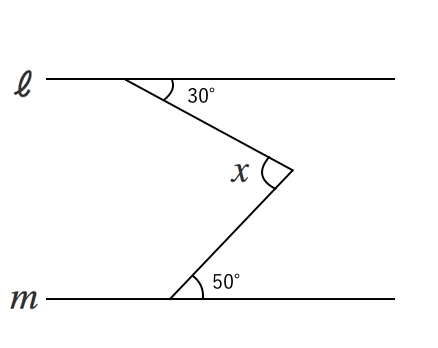
作図角度15°・30°・45°・60°・75° 中1方程式一次方程式の解き方をまとめておくよ! 中1 作図円の中心を求める方法を解説! 数学Ⅰ(abc)二乗の展開公式は?問題の解 正負の数計算の仕方(コツ)加法・減法をマスター close キーワードで記事を検索 close home図2の x の角度を求めてください。 x の先端を通り、2直線に平行な線を引くと、 平行線の錯角は等しいので、x=a+b 問題 1. 下の図で、2つの直線が平行であるとき、∠x の大きさを求めてください。 2. 下の図で、2つの直線が平行であるとき、∠x の大きさを求めてください。 (国立工業高(解説を見るだけでも応用問題の感を養うことができます.) 図において,平行線の同位角は等しいから a=45 ° x はその外角だから x=180 °−a=135 ° a=45 °で,三角形の内角の和は 180 °だから,

例題 平行四邊形求角度 Youtube
平行線 角度 問題
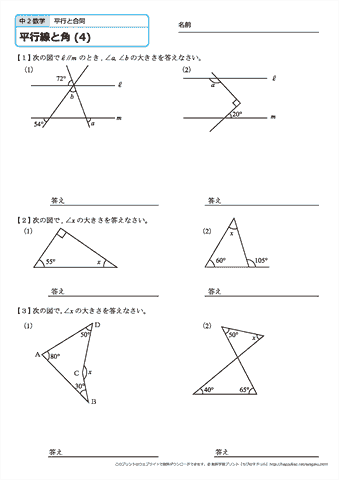
平行線 角度 問題-(十九)能了已知的函數圖形解決相關問題。 (二十)能從三角形內角和為180度及一個內角與其外角和等於180度,推得外角等於兩個內對角的和。 (二十一)能理角的種類並求出角度。 (二十二)能理解三角形的內角和定理:三角形內角和為180度。丸付けをして、間違えた問題はもう一度やり直したり、解説を理解していこうね。 1. 次の各問に答えなさい。 (6点×2問=12点) 解答 (1) 内角の和が1260°の正N多角形のNを求めなさい。 (2) 1つの内角が165°になる正多角形を求めなさい。 2. 次のそれぞれのxの角度を求めなさい。(6点×4問=24点



东阳初一数学期末考试最后一题 平行线有关的角度问题 编的真巧 图片 蛋蛋赞
(八)能應用等差數列解決生活中的問題。 (九)能知道a、b、c三數成等差數列,則b稱為a、b、c 的等差中項;並能應用公式b=(a+c)÷2解題。 (十)認識等差級數,並能從少數項的實例中,理解等差級數n項和的求法。 (十一)能推導出等差級數n項和的公式Sn=n(a 1+a n)÷2,並應用公式解題数学24章図形の調べ方「平行線と角」<基本問題②・解答> 1 解説 (1)多角形の外角の和は360°であるから ∠x = 360°-(105°+95°+1°)=40° ※四角形の内角の和が360°であることから求めてもよい。 (2)三角形の1つの外角は,そのとなり にない2つの内角の和に等しいので ∠y =125°-55°-30外部リンク スウガクとくガウス ラングレーの問題の項に、整角四角形問題に関する詳しい記述がある。;
(八)能應用等差數列解決生活中的問題。 (九)能知道 a、b、c三數成等差數列,則b稱為a、b、c 的等差中項;並能應用公式b=(a+c)÷2解題。 (十)認識等差級數,並能從少數項的實例中,理解等差級數 n項和的求法。 (十一)能推導出等差級數 n項和的公式S n=n(a 1+a n)÷2,並應用公式角度の表し方(復習) 図1の赤で示した角は半直線baとbcでできている。 このba、bcを角の辺といい、点bを 角の頂点 という。 この角を表すには∠b、または∠abcと書く。 ∠abcのように3文字で表す場合は 角の頂点の文字 bを必ず中央 に書く。 bを中央にすればいいので∠cbaと書いても平行線と角度5 小学校4年 算数 中学受験
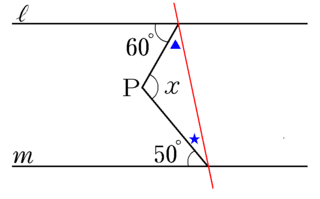
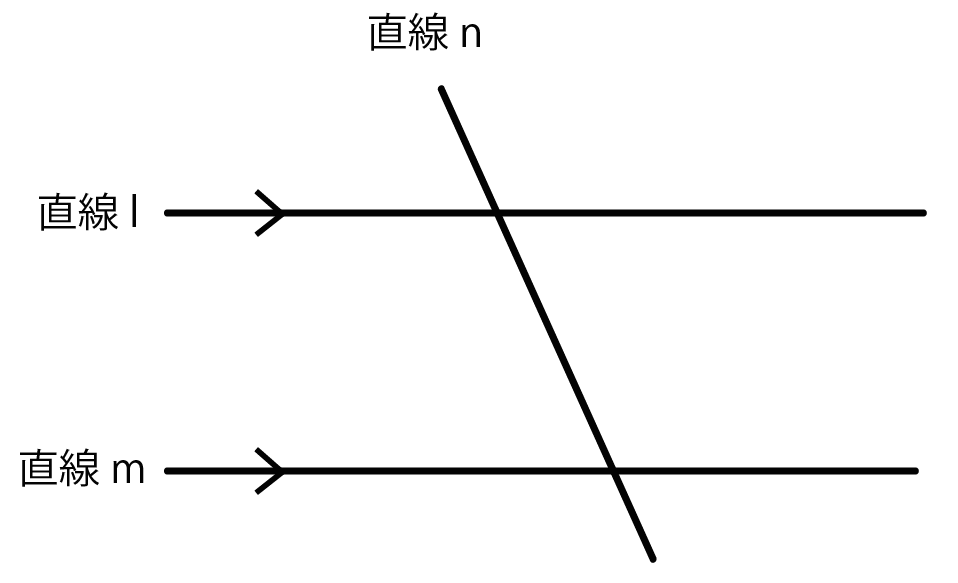
この問題は、現多良木中学校 毎床教頭から出していただき、私がちょっと悩んだ 問題です。 中学校の知識で解決できます。三角関数を利用して解決した先輩もいらっしゃ いましたが・・・ 皆さんもちょっとチャレンジしてみて下さい! 1.次の図のような平行四辺形ABCDで、角χの大きさを 補助線は、問題の中に 角ができる点に注目し、 L、M と平行で それらの点を通る線を 引きます。 そうしますと、あちらこちらに錯角やら同位角があらわれ、 図の中に現れるすべての角度が計算できます。 この考え方と、計算の仕方は ほとんどの平行線 併せて、対頂角となる②も角度は等しいことから、①②③は全て同じ角度となり、平行線の同位角、錯角、対頂角が等しいことが分かります。 この説明を証明と捉えて良いと思います。 平行線公準問題に対する取り組み期間はフェルマーの最終定理の比ではなかった ウィキペディアにある、



悟空问答 七年级下册 人教版 数学实数应该怎样攻破 6个回答



角度を求める 補助線 Takapの数学日記
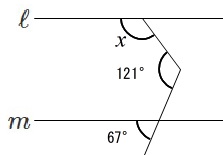
平行線與橫向線形成的角度 (英) 平行線成的角度 上傳 × 謝謝您協助我們回報問題 我們已經收到您回報的問題,同時也將回報的內容寄到您的信箱。如果需要進一步資訊,我們會透過您所填寫的 Email 與您聯絡。 我們會儘速處理您所回報的問題,如果您有任何問題,歡迎利用 support@junyiacaemyorg問題作成のご要望を募集しております。掲示板にお書き こみください。 算数問題データ 算数 角度調査の学習教材・問題集です。以下からページ番号ををご選択ください。 角度を調べよう3平行線の角度を調べる問題p001同じ角度なら、平行』 ということだけおさえておけば、 今後の問題を解くための「使える武器」になりますね! もちろん、下図のような「平行ではない場合」でも 「同位角」、「錯角」と言いますが、 問題では、9分9厘「平行」ですね!
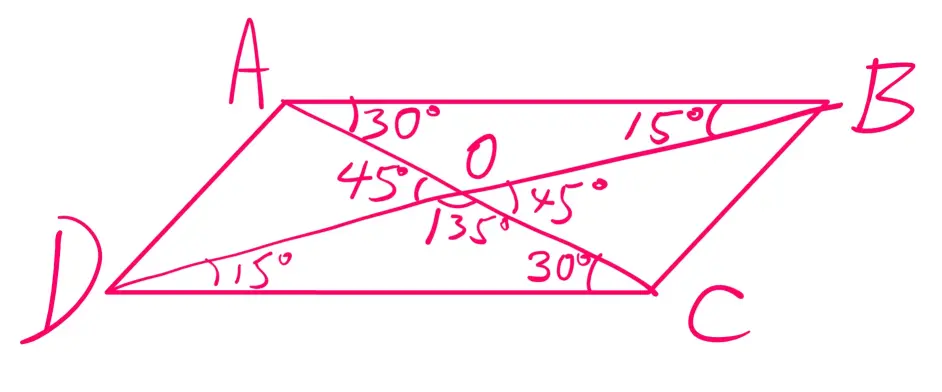



求角 Dac 平行四边形性质定理与各种角的和差关系都试过 也搞不出来 哔哩哔哩



初中數學 梯形的五種常用輔助線添加方法 17道例題詳解培優幾何 雪花新闻
いろんな角度を作図する方法を解説! 長方形・正方形の折り目を作図する問題を解説! 3辺から等しい距離にある点の作図方法を解説! 円の中心を作図する方法を解説! 円の接線作図!基本から2つの円の共通接線は? 円に内接する正三角形の作図方法とは?中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷 ;角度の難問1 中学受験専門塾・優学習会 すぐるホームページ > すぐるゼミ > 算数 > その他 > 難問集 > 角度の難問1 問題



図形の調べ方 角度を求める問題 苦手な数学を簡単に
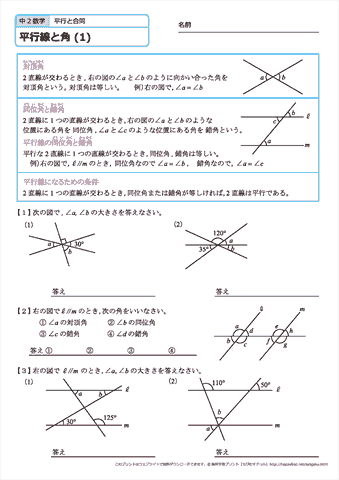



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
/中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおしながら左クリックすると,新規ウィンドウが開きます 数学: 数学1 年,数学2 年,数学3 年 (Shift+左由平行線與橫向線所形成的角度 (英) 平行線、橫向線、等位角 由平行線與橫向線所形成的角度 (英) 平行線、橫向線、等位角 上傳學習單 下載學習單 你喜歡這支影片嗎? 快來幫這支影片打分數吧! 你不喜歡的原因是?平行線の錯角・同位角 基本問題 図でl // mである。 それぞれ∠xの大きさを求めよ。 l m 66° x l m 74° x x 87° l m 152° x l m 56° x l m l m x 97° 図でl // mである。 それぞれ∠xの大きさを求めよ。 l m 58° 52° x x 68° 64° l m x l m 53° 81° 1③⑥の解説 2③の解説 解説



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく




看似零散的平行四邊形 都是圍繞著這三個方面出題 每日頭條
Title いろいろな角度の問題xls 互換モード Created Date PM中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード・印刷 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要領(21中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード・印刷 ;



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1
平行線 在歐幾里得空間中,直線的方向向量是一個單位向量 ,使得原點到直線上所有點的向量都能表示為 , 。 若干個由方向向量,,, 確定的直線相互平行若且唯若這些向量全部相等或只差一個正負號。 在歐幾里得空間中,平面的法向量是一個單位向量 ,使得平面上所有的向量都與 垂直。四角形の性質 平行線と面積1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 平行線と面積1 名前 右の図でAD//BCの中学受験 算数 動画解説 平面図形5 角度⑤ 平行線と角制作者のホームページは http//kyoikuinfo



平行线的最复杂计算 西瓜视频搜索




中学入試 ありがちな平行線の角度問題ですが 暇つぶしに動画で脳トレ
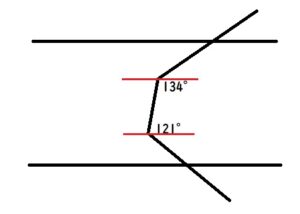
工夫していろいろな角度を求める問題で、平行線の錯角や同位角が等しい性質、三角形の角の性質を使う問題です。 よく出る問題で練習してから応用問題に取り組んでいくようにしましょう。 平行線の角度の性質を使った問題 例)矢印のつ(八)能應用等差數列解決生活中的問題。 (九)能知道a、b、c三數成等差數列,則b稱為a、b、c 的等差中項;並能應用公式b=(a+c)÷2解題。 (十)認識等差級數,並能從少數項的實例中,理解等差級數n項和的求法。 (十一)能推導出等差級數n項和的公式Sn=n(a1+an)÷2,並應用公式解題角度の難問 (中学生版) 1 /32 問題 AB=ACの二等辺三角形 ABC があり,角Aは ° です。 いま,辺 AC 上に点D,辺 AB 上に点Eがあり,DからB,EからCに直線を引いたところ,角 DBC = 60° ,角 ECB = 50° となりました。 DからEまで直線を引いたとき,角 BDE (図のχ




例題 平行四邊形求角度 Youtube




角度の問題まとめ 無料で使える中学学習プリント
系統思考與解決問題 b1符號運用與溝通表達 b3藝術涵養與美感素養 c1道德實踐與公民意識 課程目標: (一)能觀察生活中的有序數列,理解其規則性,並認識「數列、首項、第n項、末項」等名詞。 (二)能察覺不同的數列樣式彼此間的關係。2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習指導要領



平行線の同位角と錯角を利用して角度を求める問題の解き方




旋轉卡尺 Hackmd
演習問題に たくさん取り組んで、 短い時間で 図形のパターンを 見つけ出して ルールが使えるように、 練習してみて下さい。 まとめ 三角形と平行線の線分の比について まとめます。 1.三角形と平行線の線分の比のルール(八)能應用等差數列解決生活中的問題。 (九)能知道a、b、c三數成等差數列,則b稱為a、b、c 的等差中項;並能應用公式b=(a+c)÷2解題。 (十)認識等差級數,並能從少數項的實例中,理解等差級數n項和的求法。 (十一)能推導出等差級數n項和的公式Sn=n(a1+an)÷2,並應用公式解題




七年级数学 平行线辅助线做法几大总结 赶紧收藏学习一下 网易订阅



北师大版七年级下册数学期中 三角形中的角度问题 高 角平分线 哔哩哔哩 つロ干杯 Bilibili




七年级数学 平行线辅助线做法几大总结 赶紧收藏学习一下 网易订阅




几何我讲数学 Beo Play官网




旋轉卡尺 Hackmd
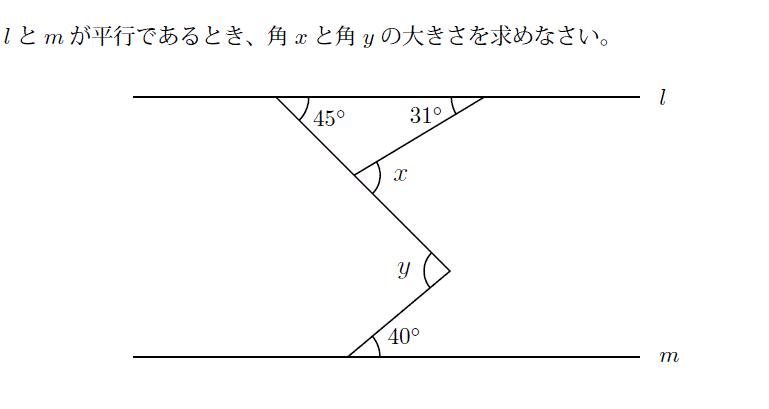



かみのドリル 角度



东阳初一数学期末考试最后一题 平行线有关的角度问题 编的真巧 图片 蛋蛋赞



初一数学 期末押题 角度之间的关系 专题复习 模型



贞元讲座 初中数学只能刷题吗 玩游戏 学数学 初中版 知乎



妙添辅助线 巧证角相等 西湖数论之我来讲题 第168期 西湖数论 微信公众号文章阅读 Wemp



中学2年平行線と角度の問題です 直線l Mが平行のとき xの角度 Yahoo 知恵袋



算数4年 上 第3回 応用問題解説 最難関問題集 予習シリーズ解説ブログ



函数与方程的五个命题角度 教育频道 手机搜狐




初一数学下册 探究平行线出现拐点构成的角度问题 利用方程思想解题 知乎



在cad中画平行线 西瓜视频搜索



平行線と角度 中学から数学だいすき



1




図形問題の補助線 平行線 東久留米 学習塾 塾長ブログ



平行 维基百科 自由的百科全书
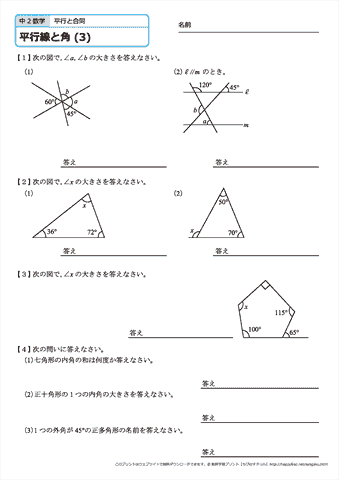



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
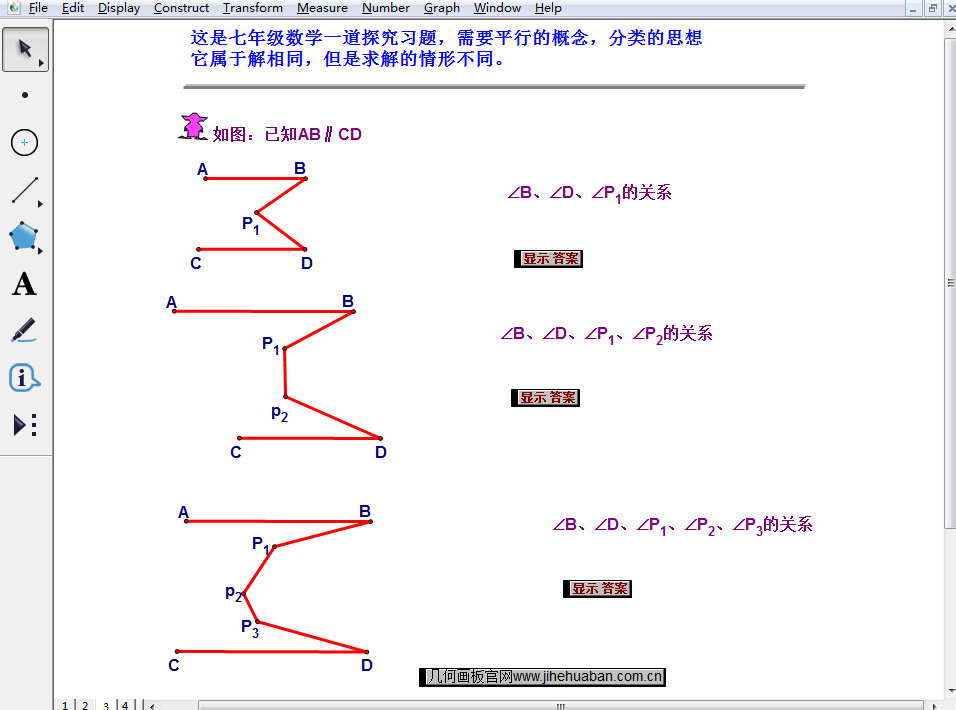



利用几何画板探究平行线开放性问题



平行線を利用する角度問題の基本 広尾学園中学 2010年 全国180中学の入試算数 解法研究




東陽初一數學期末考試最後一題 平行線有關的角度問題 編的真巧 每日頭條




飛鏢模型 原來這麼簡單 四種方法都非常棒 壹讀




初一数学 角度的n等分线 结合平行线间的拐点问题 知乎



Q Tbn And9gcsszp Cxkda Husd8cdymubkkbpunasilb8yejz6zs7oiaevmr6 Usqp Cau
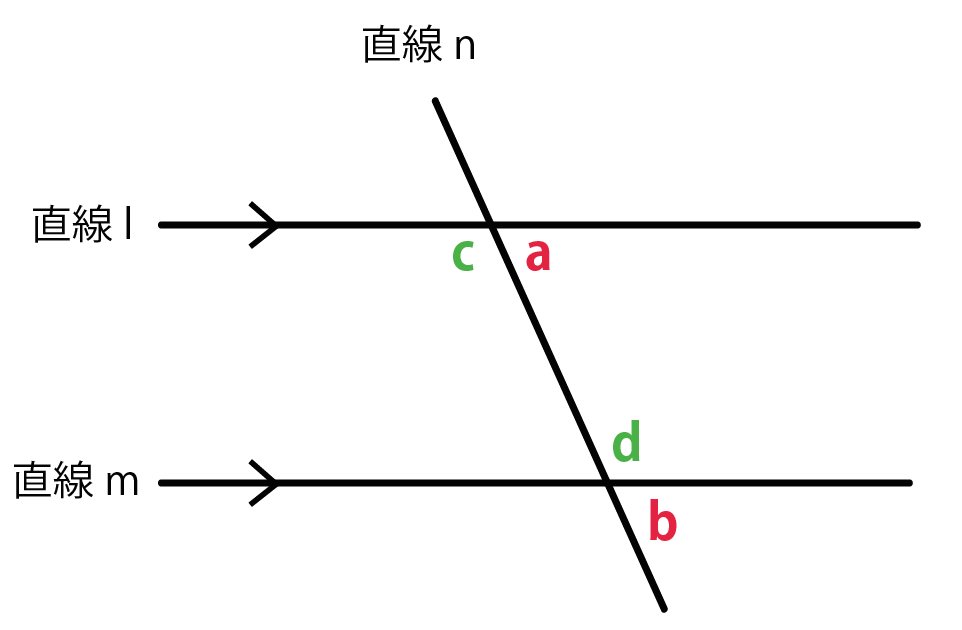



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく




多角度带你玩转菱形存在性问题 平行线教育官网



5 2平行四边形的判定 1 教学思路及教后感 数海贝童 微信公众号文章阅读 Wemp




平行線的意義截線與截角平行的判別平行的應用自我評量 Ppt Download
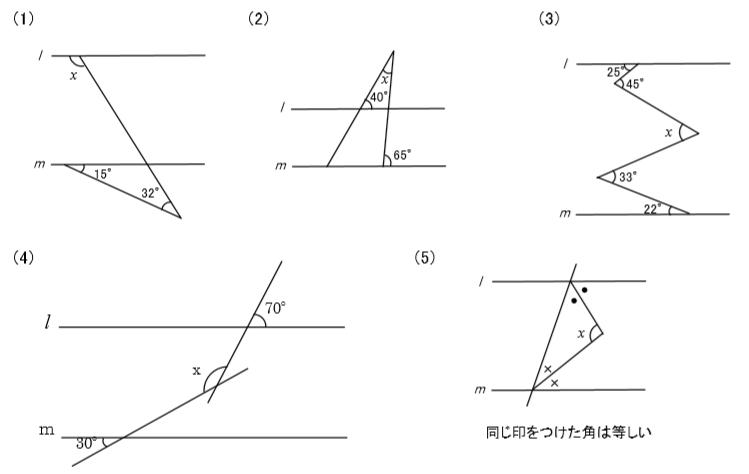



中2数学 対頂角 同位角 錯角と平行線の関係のポイントと練習問題 Pikuu
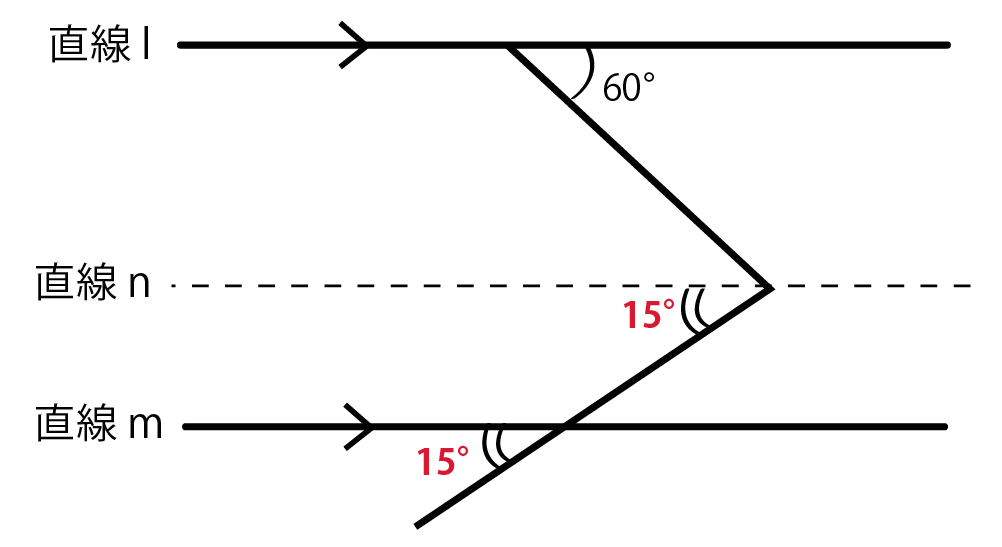



同位角 錯角 平行線の性質で問題を2秒でクリアする方法 Qikeru 学びを楽しくわかりやすく




例題7 平行線與角度問題 Youtube
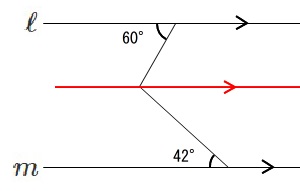



平行線の同位角と錯角を利用して角度を求める問題の解き方
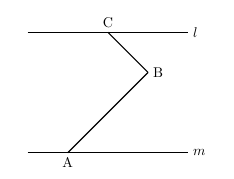



平行線と角の問題の解法 夢を叶える塾
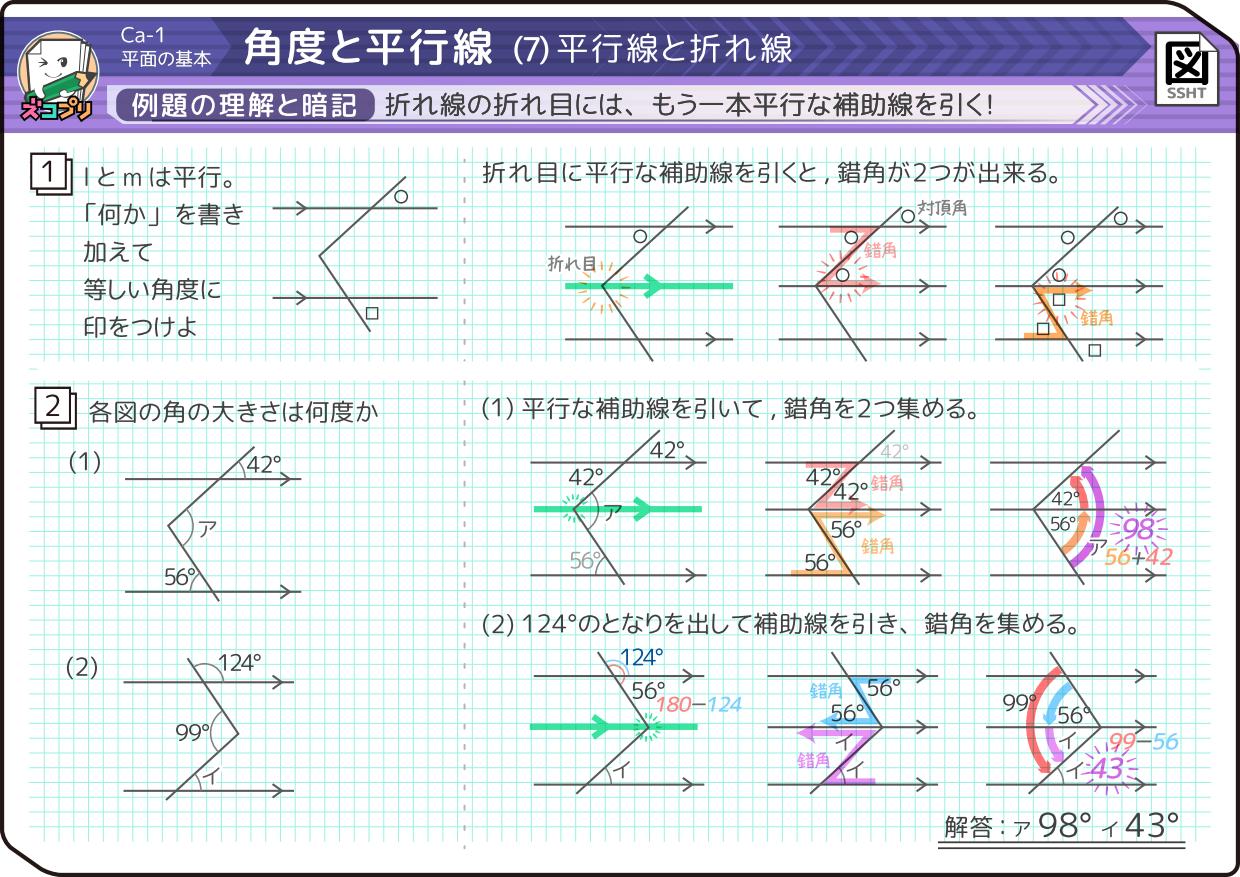



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



中2数学の平行線と角の所の問題なんですが この画像のxの角度を Yahoo 知恵袋




中学入試問題 ありがちな平行線の角度問題ですが 暇つぶしに動画で脳トレ



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分
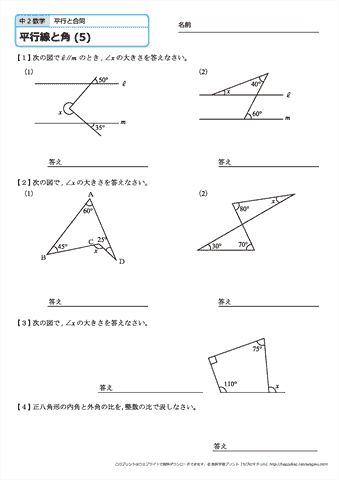



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
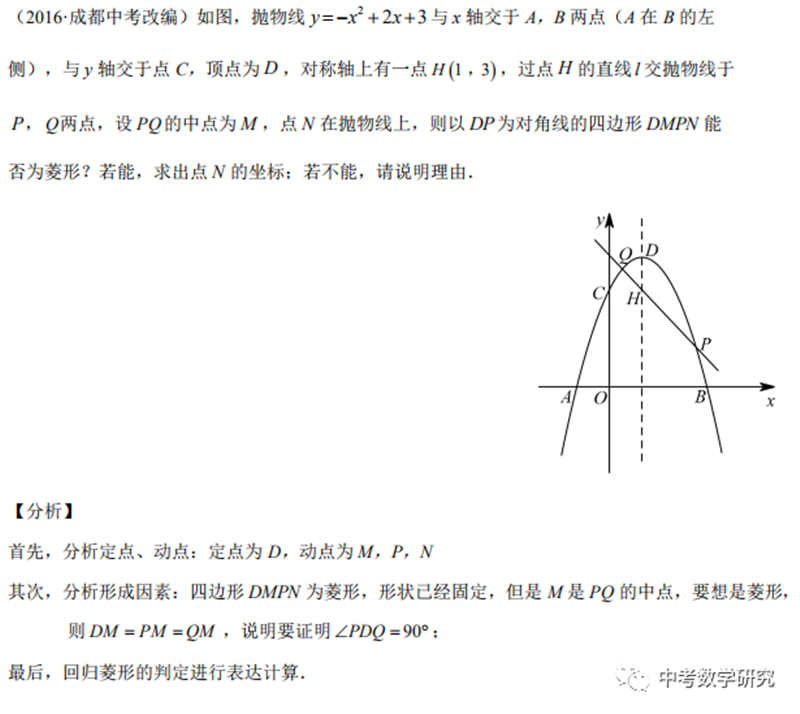



多角度带你玩转菱形存在性问题 平行线教育官网
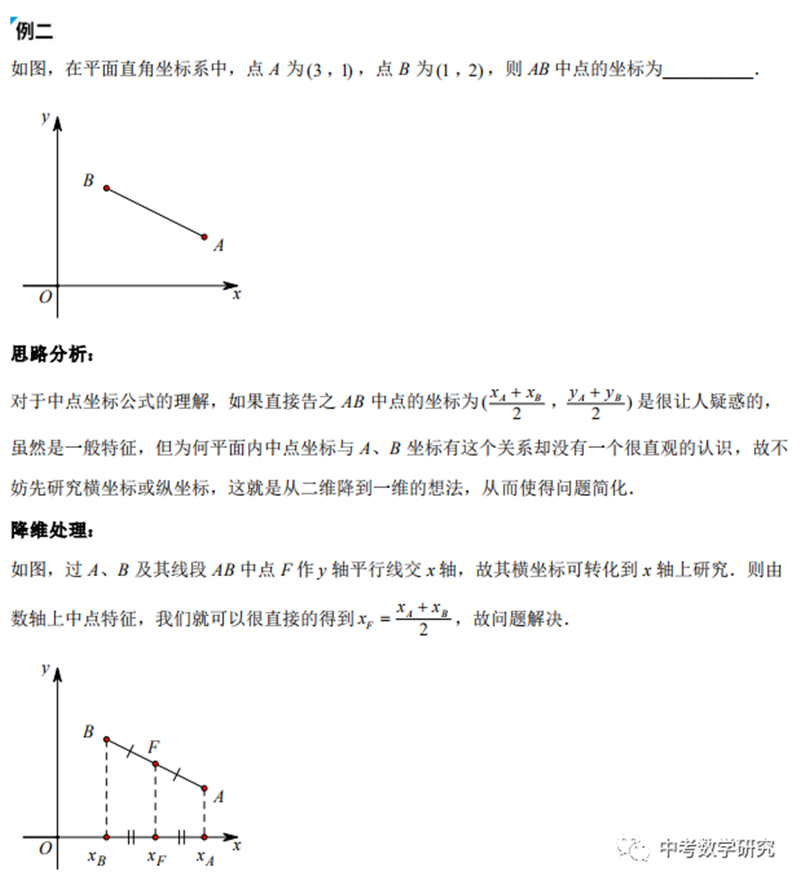



数学中的 升维思考 降维解题 平行线教育官网



平行线怎么画画垂线与平行线教学反思三篇 学习岛




Ppt 几何初步及平行线 相交线powerpoint Presentation Free Download Id
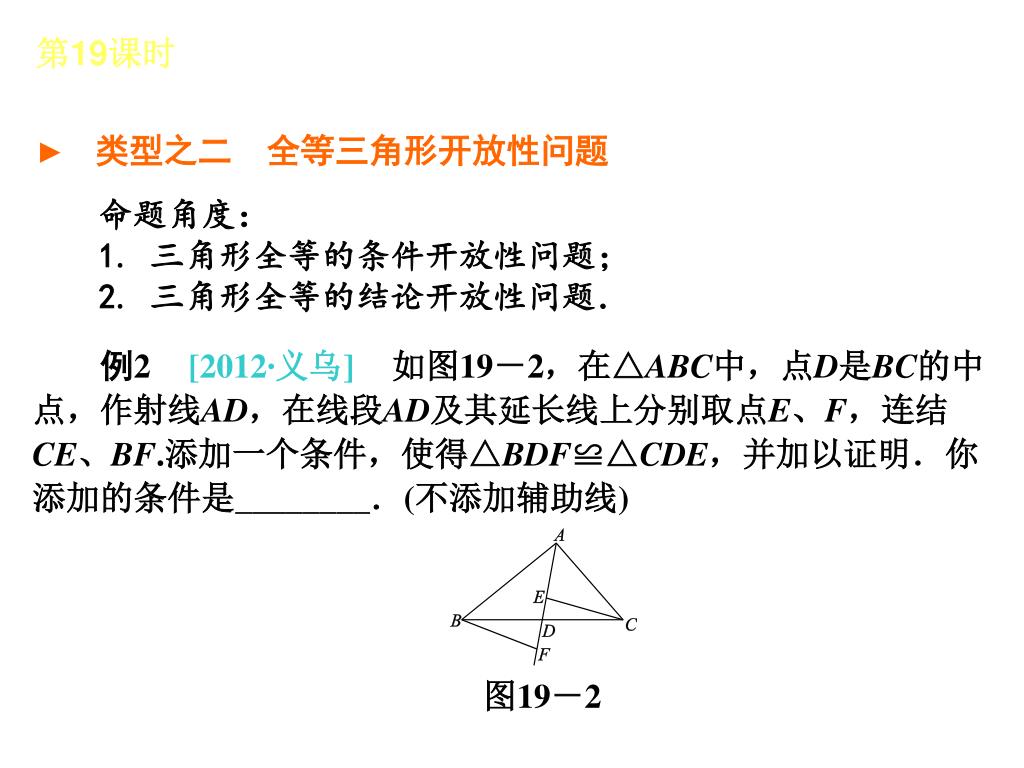



Hd限定三角形角度問題 最高のカラーリングのアイデア




平行线的判定与性质练习题 几何图形问题第1题 初一数学练习题 每周练习 数学周周练



平行线的最复杂计算 西瓜视频搜索



妙添辅助线 巧证角相等 西湖数论之我来讲题 第168期 西湖数论 微信公众号文章阅读 Wemp



七下数学旋转 西瓜视频搜索




対頂角 平行線の角 同位角 錯角 無料で使える中学学習プリント




中考數學壓軸題 平行線這樣解答一定得高分 每日頭條
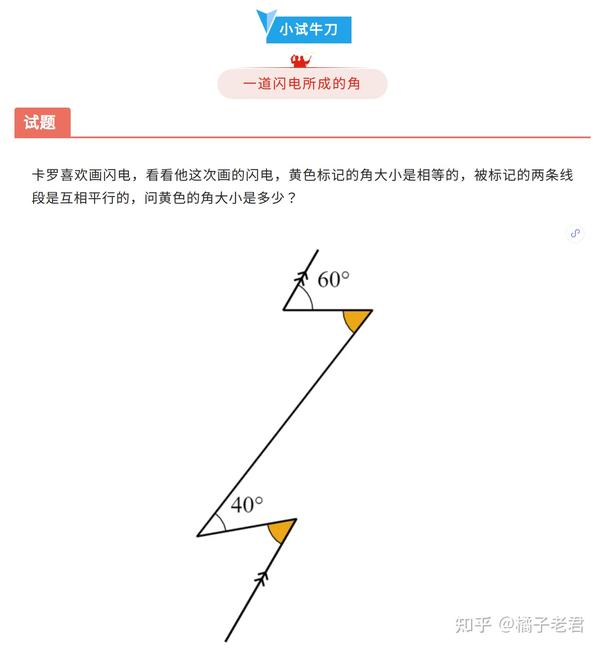



角度问题系列 知乎
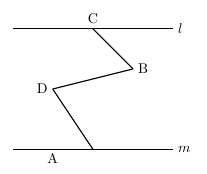



平行線と角の問題の解法 夢を叶える塾
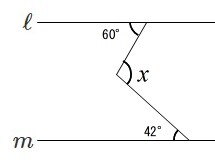



平行線の同位角と錯角を利用して角度を求める問題の解き方




Hd限定三角形角度問題 最高のカラーリングのアイデア



正方形与平行线角度问题 俄罗斯趣味题一则 补充了解法 彭翕成 新浪博客




易百分國中數學 奇士老師 平行線與截角問題 平行移動求角度 Youtube




鲁教版七年级初一数学下册 平行线的有关证明6 三角形内角和定理的证明 教材教案word 牛图文 第8页



Q Tbn And9gcsbbbelxvzd0wwnjbk65sm2w3ughnrm43c9jen5ens Usqp Cau




平行线可以相交 俄国数学天才将其发现却遭讽刺 死后才得以证明 网易订阅
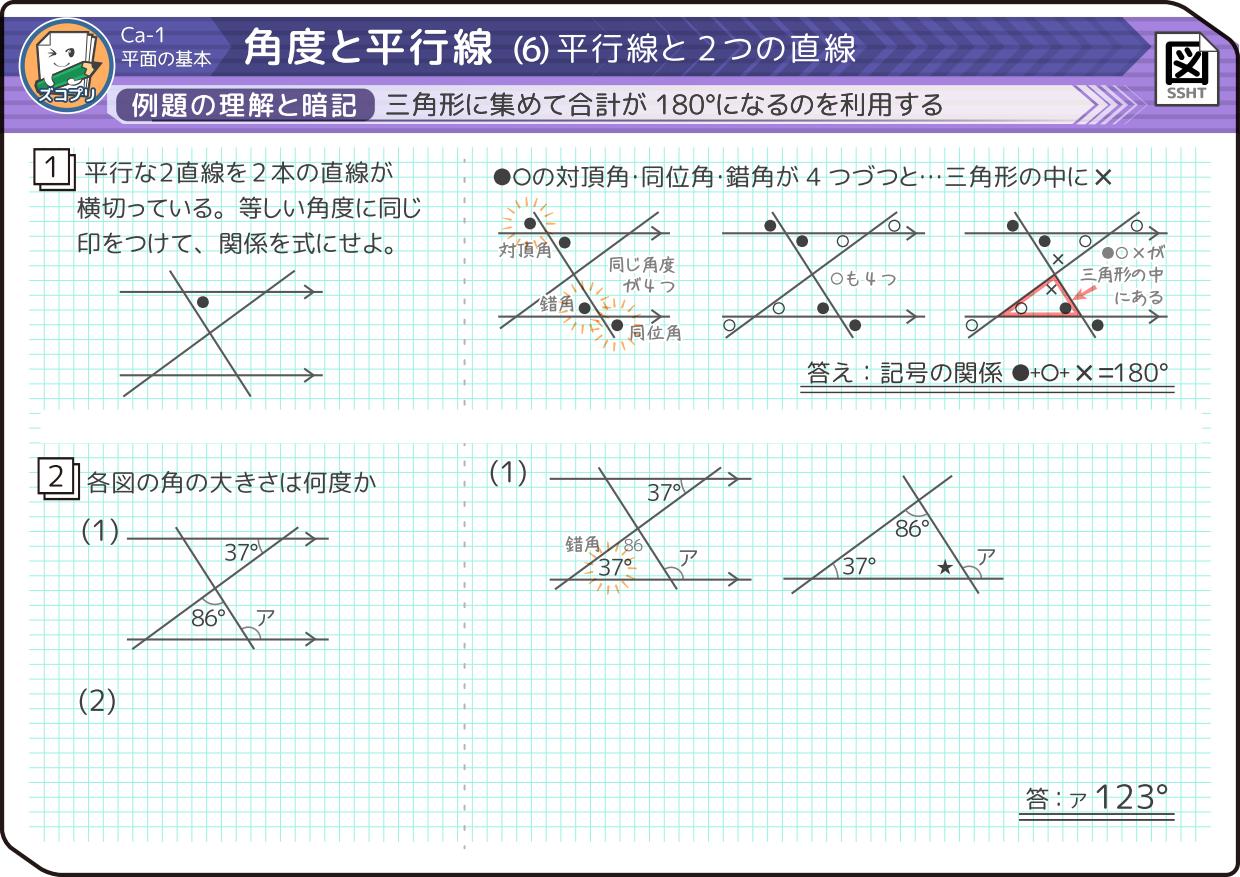



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



中考数学复习 这三类解直角三角形的应用套路 你了解多少呢



利用平行线的性质求角度问题 哔哩哔哩 Bilibili
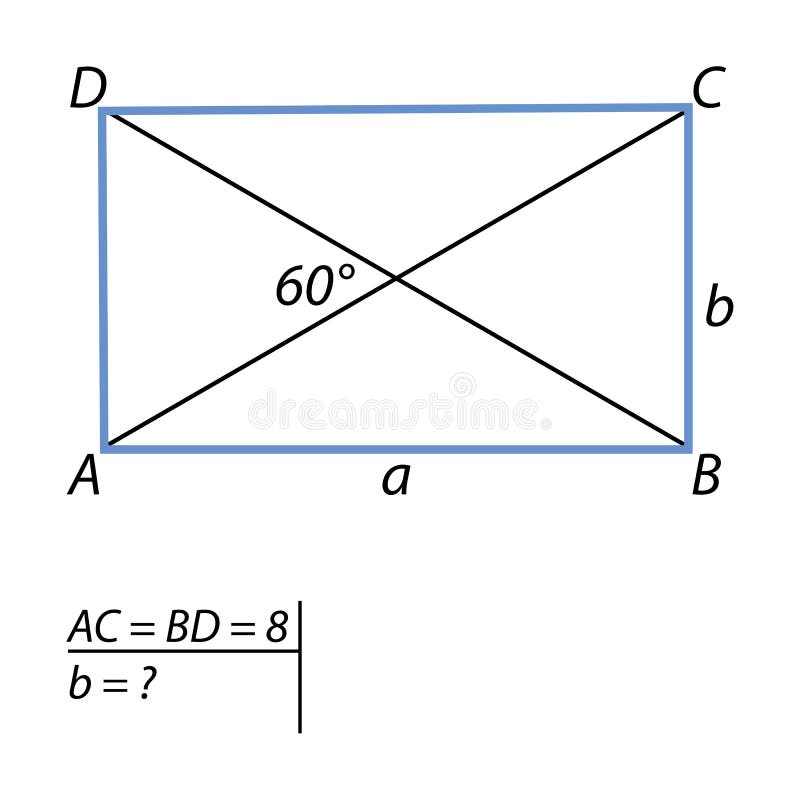



任务发现短的旁边平行四边形向量例证 插画包括有 2130
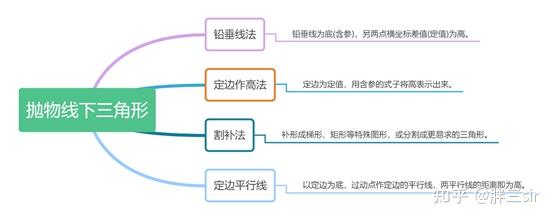



中考数学 抛物线专题1 抛物线中三角形面积的最值问题 知乎




大咖分享 一个求角度问题的多种解法 平行线教育官网




大咖分享 一道imo数列问题的背景探究 平行线教育官网
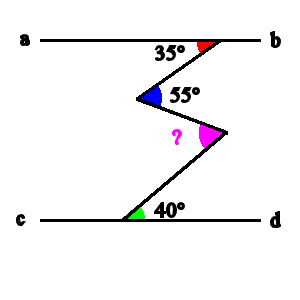



同位角錯角の問題




對角線垂直平分的菱形 除了四條邊相等還知道那些 每日頭條




Hd限定三角形角度問題 最高のカラーリングのアイデア
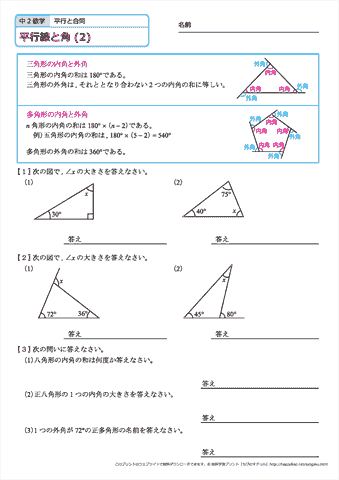



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
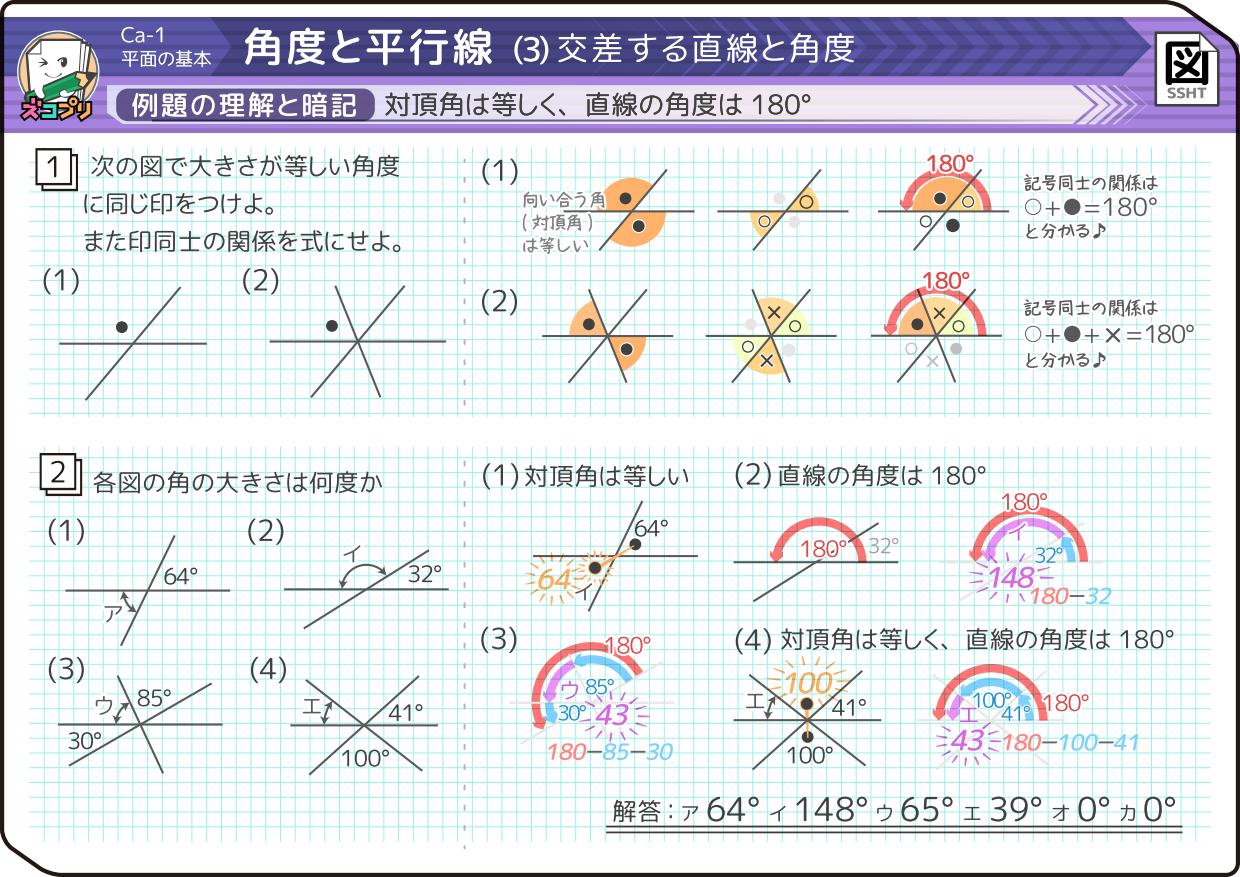



小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ



空间直线角度相关问题 哔哩哔哩 つロ干杯 Bilibili



Studydoctor平行線と補助線の問題 中学2年数学 Studydoctor
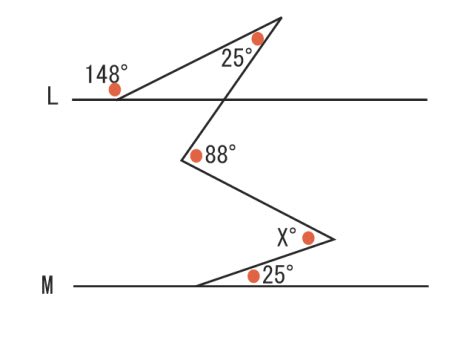



平行と 角度 の 問題 補助線の引き方は 名寄 算数数学教室より



平行線と角度 中学から数学だいすき



东阳初一数学期末考试最后一题 平行线有关的角度问题 编的真巧 图片 蛋蛋赞



求角度 腾讯视频
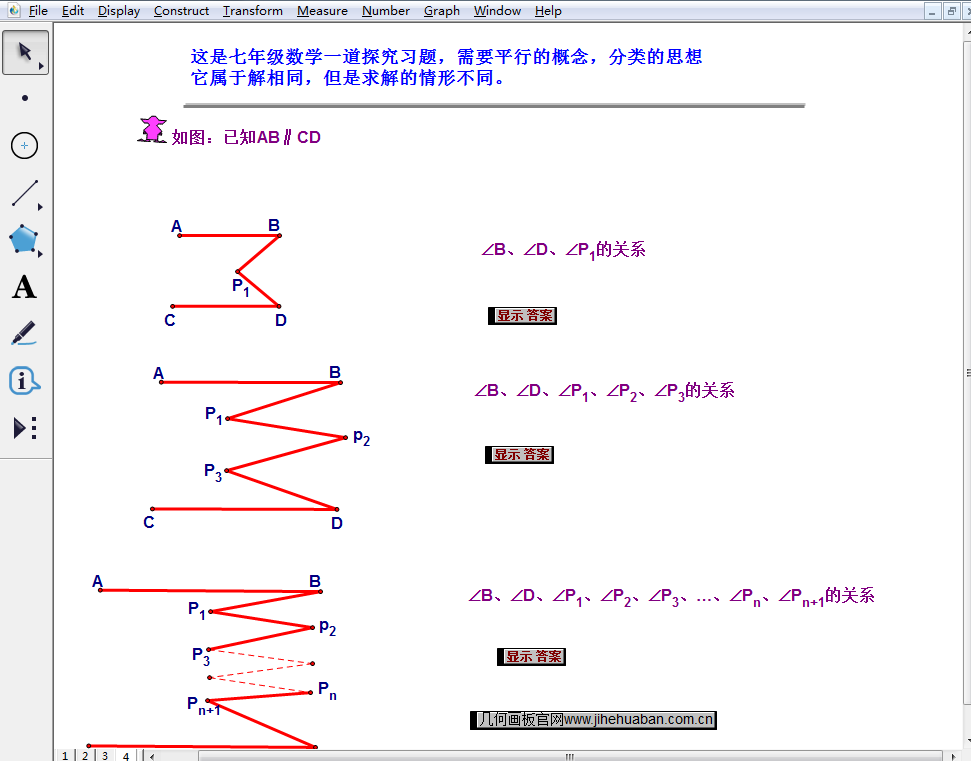



利用几何画板探究平行线开放性问题
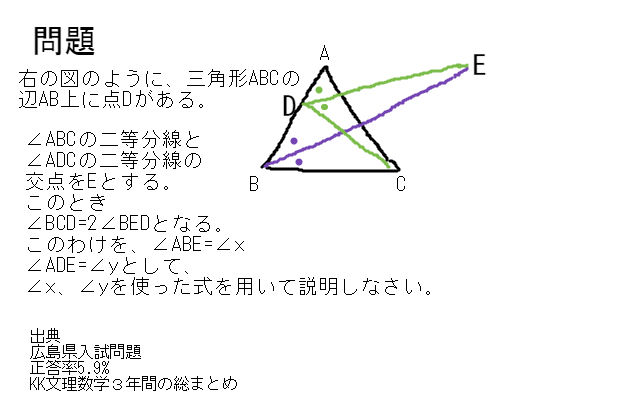



正答率5 9 の問題 平行線と角 チャレンジを 制限3分 中学数学 理科 寺子屋塾の復習サイト




在模型化思想下用角度关系处理立体几何问题 参考网




平行线上的角 在普通支票左上角划两条平行线的划线支票只能用于转账 三人行教育网 Www 3rxing Org




两平行线之间的角度关系 Cad里面怎样标注倾斜的两平行线之间的距离 未知角度 三人行教育网 Www 3rxing Org




角度を求める イナズマ型 Next Stageのブログ




平行線的意義截線與截角平行的判別平行的應用自我評量 Ppt Download




初一数学 角度的n等分线 结合平行线间的拐点问题 知乎
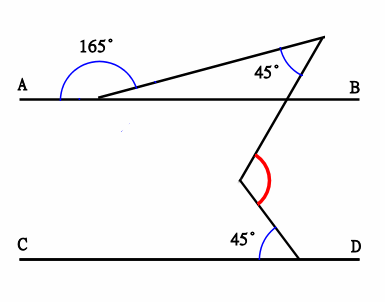



同位角錯角の問題




平行と 角度 の 問題 補助線の引き方は 名寄 算数数学教室より



0 件のコメント:
コメントを投稿