垂直二等分線の書き方 中3数学 1 代入前に整えろ!式の値を求める応用問題の解き方 中3数学 計算公式立方体の対角線の長さの求め方がわかる3ステップ 中3数学 中学数学三角錐の高さの求め方がわかる4つのステップ小学6年生 速さ・時間・道のり 練習問題プリント① 「速さ」の公式と問題の解き方のポイント|小学生に教える 速さ、距離、時間の公式と求め方 スタディビジョン;3月 小学1年生 ‶考える力"を育てる! 小学3年生 10までの数(数の数え方、読み方、書き方、数の並び、0という数) なんばんめ(順序や位置を数で表す)/いくつといくつ(5~10の数の合成・分解) 1桁のたし算(和が10以内のたし算)/1桁のひき算
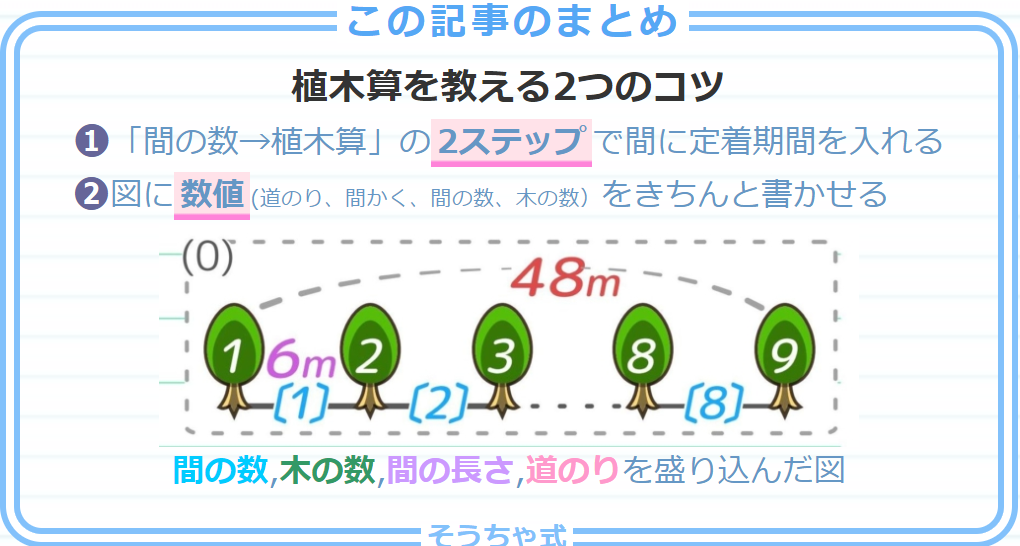
中学受験 植木算の教え方の2つのコツ 小学3年生にも分かりやすい そうちゃ式 受験算数 新1号館 数論 特殊算
道のりの求め方 3年生
道のりの求め方 3年生-求め方① 秒あたりに進む道のりを求める。 こうすけ: ÷= ( ) 秒あたり( )m のぶたか: ÷ 5=( ) 秒あたり( )m 求め方② mあたりにかかる時間を求める。 こうすけ: ÷ =( ) mあたり( )秒 年生 速さ 4 3学習日 年 月 日 1.速さを求めましょう。 (1)1㎞を2時間で進んだ電車の時速 (2)180mを6分で進んだ自転車の分速 (3)240mを12秒で走った電車の秒速 2.道のりを求めましょう。 (1)時速32㎞の人が5時間に歩く道のり (2)分速900mの馬が3分間走る道のり
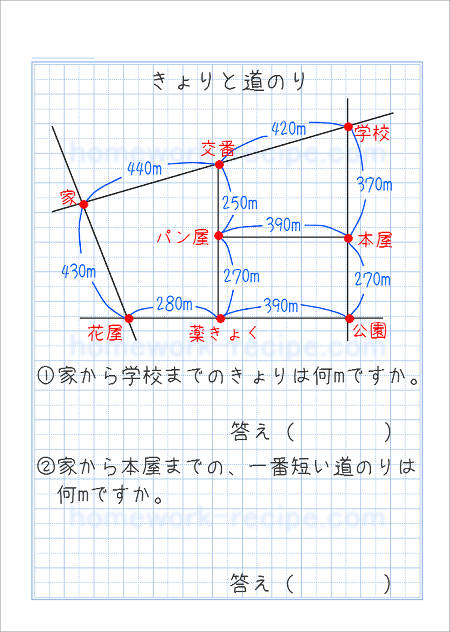



きょりと道のりの練習問題 家庭学習レシピ
高校入試の肝! 「数学」最短距離の求め方 静岡県私立高校入試 (21年2月2日・3日)が近づいて参りました。 そこで、受験直前の中学3年生応援企画として、おさえておきたい頻出問題の解法について、ワンポイントレッスンしていきます。 今回は「数学道のりや時間の求め方については,既習内容である速さの公式や図を基に分かりやすくさ 17年の世界陸上で金メダルをとった選手の記録に6年生は勝てるでしょうか。 ただし,6年生は50mのみで競走します。 ①100m走 ②800m走 ③マラソン(42.195km) 参考 1の解説 分速を求めるには、1分間に進む道のり (距離)を出せばいいので$$600\div 5=1$$となります。 求める答えは\ (1m\)ということになります。
過去問のやり方などもアドバイスしています。 第1章 なぜ6年生になると、成績が急伸したり急落したりするのか 第2章 即効性アリ! 第9回 旅人算 74K 大人でもちょっと手こずってしまうような、難問奇問が続出する中学入試の算数。 でもだいじょうぶ、コツさえつかめば怖くありません! 学習サポートセンターのカズが、算数を楽しく学ぶ方法を伝授します。 更新 6年年5月13日水曜日 壮大 道のり 求め 方 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい 数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 速さと時間から道のりを求める問題 家庭学習レシピ
「小学3年生の算数」の教え方の例 本ページは、算数が不得意な小学3年生への教え方をQ&Aで解説しています。 ※タイトル・指導時間数・ページ・学習指導要領の指導項目については、東京書籍の「年間指導計画 略案(3年)」を参照してます。 小中学生 道のり 速さ 時間の公式を理解しよう 15年12月10日 まさお Comment Tweet Pocket 小学生で、道のりと速さと時間の公式が出てきますが、なかなか理解できずにつまづくお子さんもいらっしゃいますね。②<道のりの求め方> 秒速30mで走るチーターは,50秒で何m進みますか。 解き方 道のりを求める式「道のり=速さ×時間」を使って求める。 答 え 30×50=1500 1500m ③<時間の求め方> 時速80kmで走る電車は,240km進むのに何時間かかりますか。




往復の平均の速さ 間違えずに求められますか




3年生 算数ワーク すきるまドリル 無料学習プリント
(2)道のり、時間の求め方(2時間) (3)時速、分速、秒速の意味と求め方(1時間) (4)生活のいろいろな速さ(2時間) (5)練習とまとめ(1時間) 6 本時の学習 (1)目標 数直線や式や言葉を用いて、速さの比べ方を考え、表現することができる※この内容は移行措置により6年生から移動しています。 新学習指導要領への移行措置について 教え方4 「道のり」と「速さ」がわかっているときの「時間」の求め方をとらえさせます。 問題 速さの単元で、でてくる道のりの求め方。 道のり=速さ×時間の公式に数字を入れれば簡単に出せるのですが、結構、この公式を上手く使えないお子さんが多いものです。 速さの単元における公式は3つ。 たった3つなのですが、覚えられ




文字式 速さの問題をわかりやすく解く方法 数スタ
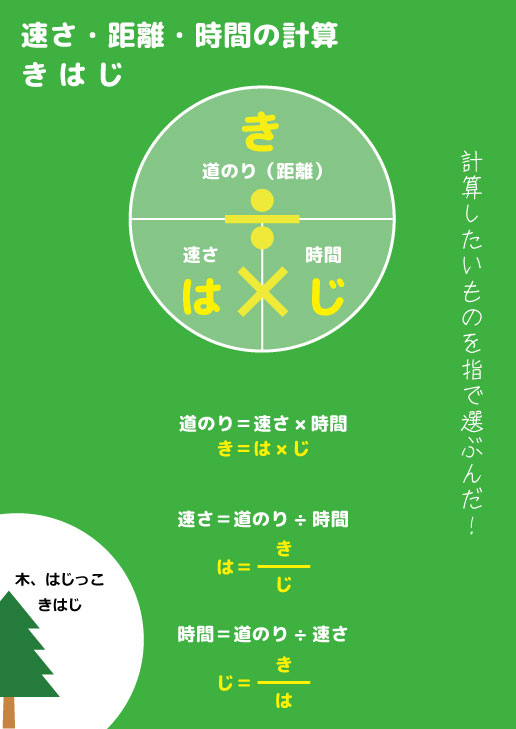



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級
1 (1)求め方(例)Aコースの道のりは,1600+1000+2700=5300で,5300mです。 Bコースの道のりは,1500+1000+3000=5500で,5500mです。 3 (1) エ (2) ウ (3) ② (4)(例)5年生と6年生で,「あてはまる」と答えた人の割合のちがいが,いちばん算数スイスイ3年生 ~小学校3年生で必ず身につけたい計算の力~ 小学校 3年 組 番 名前 草加市教育委員会 ≪草加っ子の基礎・基本≫ 算数問題集 算数スイスイ3年生 ~小学校3年生で必ず身につけたい計算の力~ 小学校 3年 組 番 名前時間=( 道のり÷速さ ) 2 次の時間を求めましょう。 (10点×2問) (1)時速50kmのバスが20kmの道のりを進む時間 20÷50=0.4 0.4= 答え 0.4時間または時間 (2)秒速80mの新幹線が48kmの道のりを進む時間 48km=48000m 48000÷80=600 答え 10分 または 600秒 1分=60秒 600÷60=10 3 秒速250mで飛ぶジェット機が




小3 算数 小3 9 球について Youtube
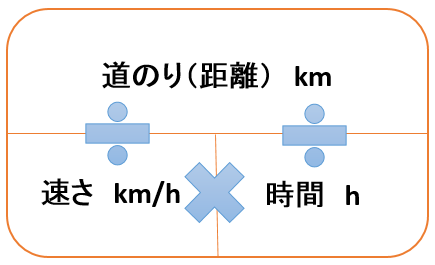



小中学生 道のり 速さ 時間の公式を理解しよう 偏差値40プログラマー
*現在プリントをリニューアルしています。かけ算のきまり かけ算のきまり かけ算のきまり 文章題時こくと時間 時こくと時間 もとめ方 時間のたんい 時間のけいさん やり方 時間のたし算、ひき算(ひっ算) 午前と午後をまたぐ時間 時こくと時間の文章題わり算 1(九九のはんいの わり算円と球 小学3年生の円と球プリントです。 こちらのプリントでは一部コンパスを使用した作図問題があります。 正確な長さを作図する能力が求められますので、 必ず100%の比率で印刷(倍等印刷)して下さい。 そうしないと1cm角のマス目が08cm角など中途教え方3 教え方3 「速さ」と「時間」を使って、「道のり」の求め方をとらえさせます。 問題 白黒ねこは、秒速10m走ります。 5秒走ったら何m(道のり)進みますか? イラスト提供元 下はそのイメージです このことから、道のりを求める式は 道のり=速さ




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




中学受験 植木算の教え方の2つのコツ 小学3年生にも分かりやすい そうちゃ式 受験算数 新1号館 数論 特殊算
3人の うち,だれが1番速く走ったかを考えます。 ② 3人の速さを求めましょう。 こうじさん (式) ゆきさん (式) けんたさん (式) ③ 3人のうち,だれが1番速く走ったといえますか。答え ① 1分間に進んだ道のりを表すときの速さ道のり・速さ・時間の求め方 道のり = 速さ × 時間 速さ = 道のり ÷ 時間求め方② mあたりにかかる時間を求める。 こうすけ: ÷ =( 3 9 ) mあたり( 3 9 )秒 のぶたか: ÷ 4 3 3=( 3 ) mあたり( 3 )秒 答え こうすけ 「速さ」をくらべているのは、求め方①です。 算数プリント 年生 速さ 4 勉強した日 月 日 4 5
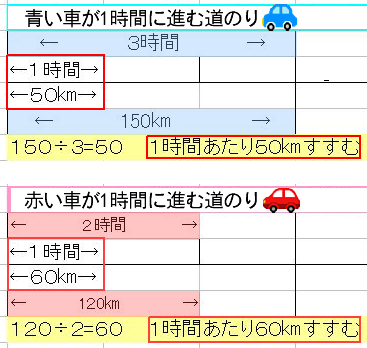



5年算数速さ 教え方のポイント



ドリルズ 小学6年生 算数 の無料学習プリント速さ 道のり
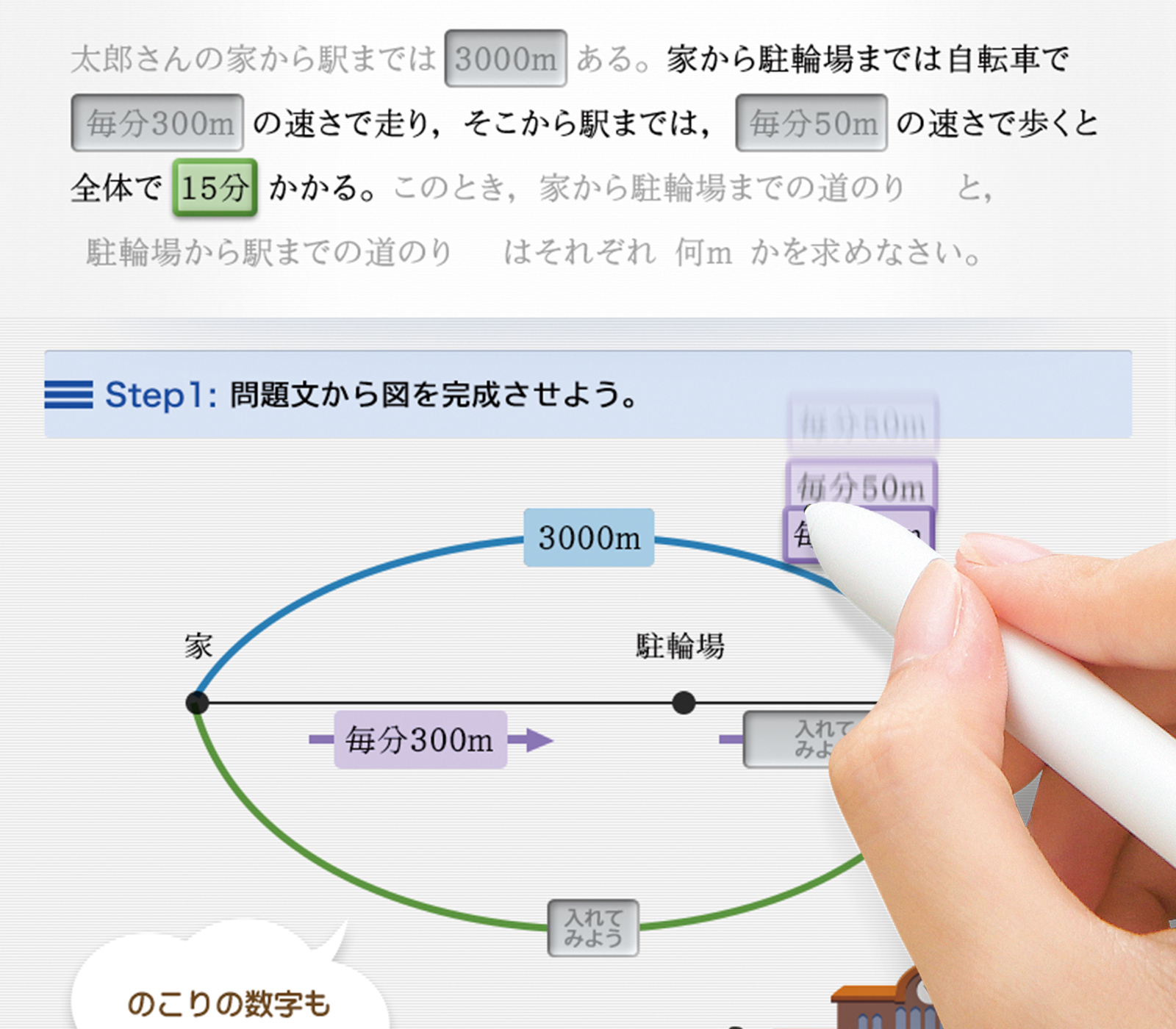
速さの意味と求め方(時速・分速・秒速) 道のりや時間を求める (9)図形の角 三角形の内角の和 多角形の内角の和 (10)倍数と約数 倍数・公倍数・最小公倍数の意味と求め方 約数・公約数・最大公約数の意味と求め方 倍数と約数の関係 偶数と奇数 素数はじきを使って時間を求める問題 分速500mで00mを進むのにかかる時間は? 時間を求めたいときにははじきを使って思い出しましょう。 つまり、距離÷速さをすればいいんだということが分かりますね。 次に問題文から距離と速さを読み取りましょうこの場合は、x,yの値がそのまま答えとはならず、x=1,y=25 を代入して求めます。 A-B間の道のり=50x この式にx=1 を代入。 方程式の解き方・等式の性質問題と解き方 中学2~3年生になっても方程式の解き方があいまいな生徒がいます。



Http Www City Soka Saitama Jp Cont S2110 Content Sansuu Suisui kaito Pdf
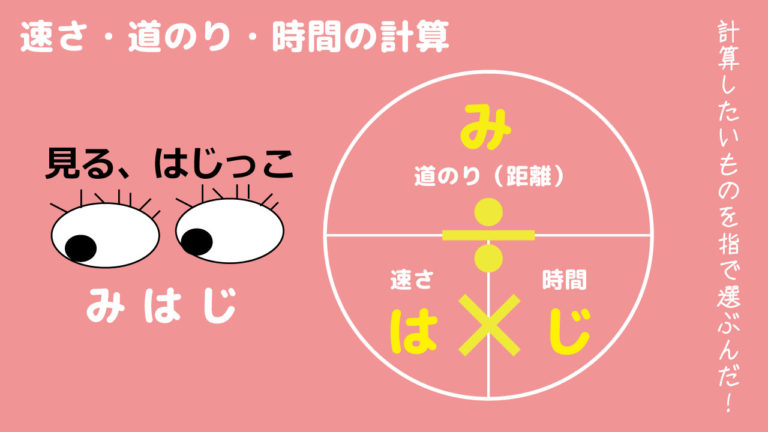



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級
時間 17秒-14秒=3秒 道のり 2m-160m=60m つまり、この列車は3秒間で60m進むので、速さは、 60m÷3秒=秒速m 続いて、列車の長さを求めます。速さを求めたので、トンネルを使っても鉄橋を使っても、普通の通過算の考え方で求められます。6年生で成績が伸び悩んだり、急落した時の学習法 第3章 6年生で伸びるための5年生での学び方 第4章 最後まで伸びる!3年生 総復習編<国語・算数・理科・社会> 漢字・言葉の学習・ を使った式/時刻と時間・音の性質/植物/昆虫・地図の決まり|小学生わくわくワーク;



算数の質問 1番右下の問題です日曜日ははじめ4分走ったから 走っ Yahoo 知恵袋



Q Tbn And9gcraww5pqgz5nz2hzprzhkk4dfl2h7cnzba1cny99bbezvcfrzxd Usqp Cau
小学校3年生 ・乗法の九九 ・整数の除法 測定値の平均 ・平均の意味と求め方 ・平均から全体量の求 め方 単位量当たりの大きさ ・混み具合の比べ方 ・人口密度の意味 ・単位量当たりの問題 を解く 速さ 比例 文字を用いた式 小学校4年生 ・整数の除法④42÷7×3=18 (分間で進む道のりを求めて3倍する) ⑤42×3=126 2時間分× 3 =7時間 126÷7=18 (時間が 時間ちょうどになるように、道 のりと時間を3倍してから速度を求める) 4 考えをクラス全体に共有し、それぞ れの解法の良さについて考える。円の面積は,次の公式で求められます。 円の面積=半径×半径×円周率 (314) (例) 半径10cmの円の面積 10×10×314=314(cm2) 1 下の形の面積を求めましょう。



2年生コース タブレットで学ぶ中学生向け通信教育 スマイルゼミ 公式 スマイルゼミ




道のりときょり 低学年の無料学習ドリル
(3) A地点からB地点を通ってC地点まで行く道のりは何kmですか。 おなじみの「坂道問題」です。 この問題は(1)→(2)→(3)のように「誘導形式」となってますので、 速さを学んだばかりの5年生にはちょうど良い復習問題 とも言えそうです。




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



1




数学 中3 14 式の計算の利用 図の証明編 Youtube



2



1
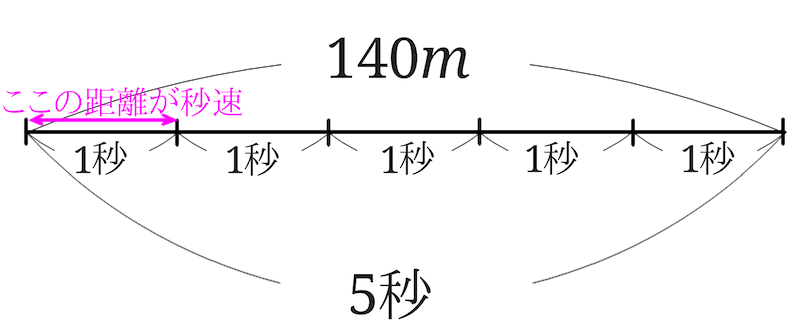



速さの求め方を時速 分速 秒速ごとに解説 みけねこ小学校




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




19年度 1学期 3年生 ニューヨーク育英学園




距離と道のり違いとは 小3算数に出てくる道のりの意味 Ruruのあれこれ日記




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい




小3 算数 小3 25 倍の計算 Youtube



小学三年生の算数です この問題の答えは何ですか 2地点の距離は Yahoo 知恵袋



Http Www City Soka Saitama Jp Cont S2110 Content Sansuu Suisui kaito Pdf
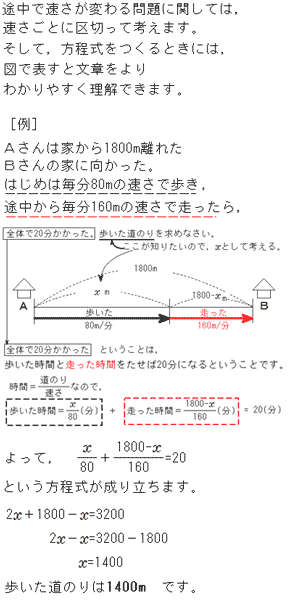



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座



文字式 速さの問題をわかりやすく解く方法 数スタ




速度問題 速さ 道のり 時間 小学6年生 算数




ボード フォニックス 英語 のピン




距離と道のり違いとは 小3算数に出てくる道のりの意味 Ruruのあれこれ日記



Q Tbn And9gcst27mhzm639xyurdznbl2orwqdq He Dni0ucc97t3hufpk2lh Usqp Cau




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




すきるまドリル 小学6年生 算数 速さ 無料学習プリント すきるまドリル 無料学習プリント



小学3年生の算数 の教え方の例 算数数学が苦手な子専門のプロ家庭教師みかん先生
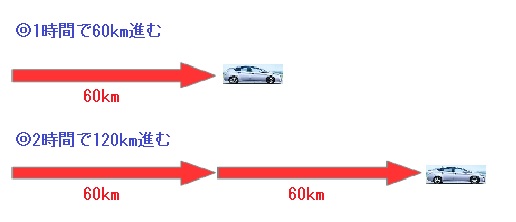



速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい




小学6年生の算数の速さのまとめ みけねこ小学校
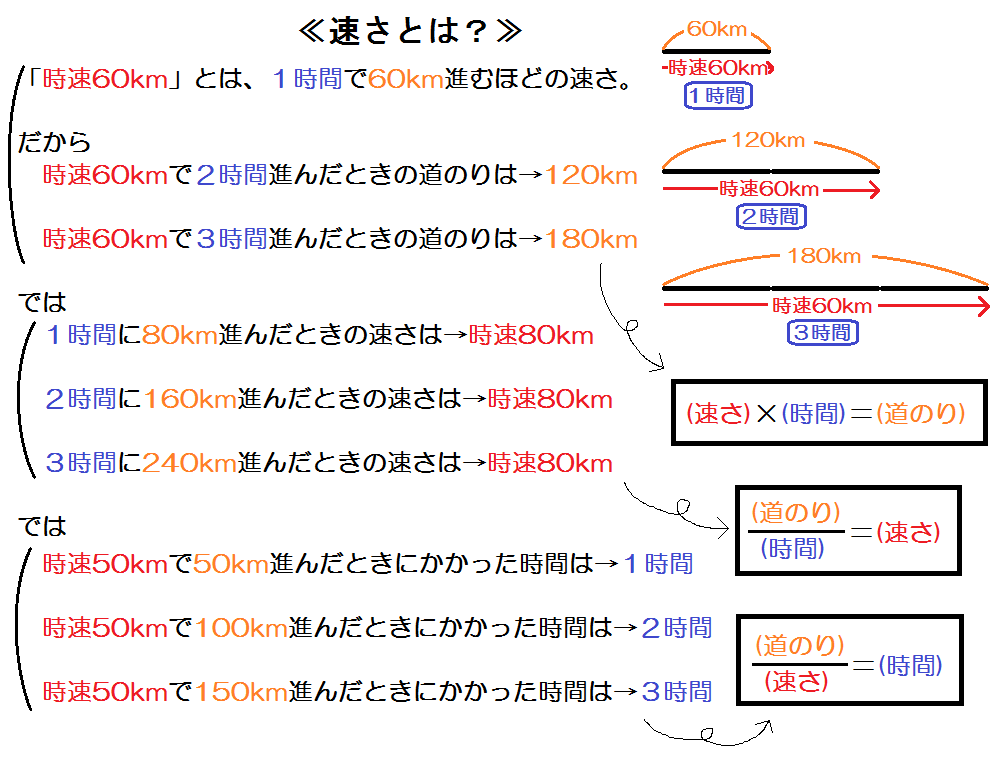



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




縮図の求め方 小6 地図などで実際の距離を計算する方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun
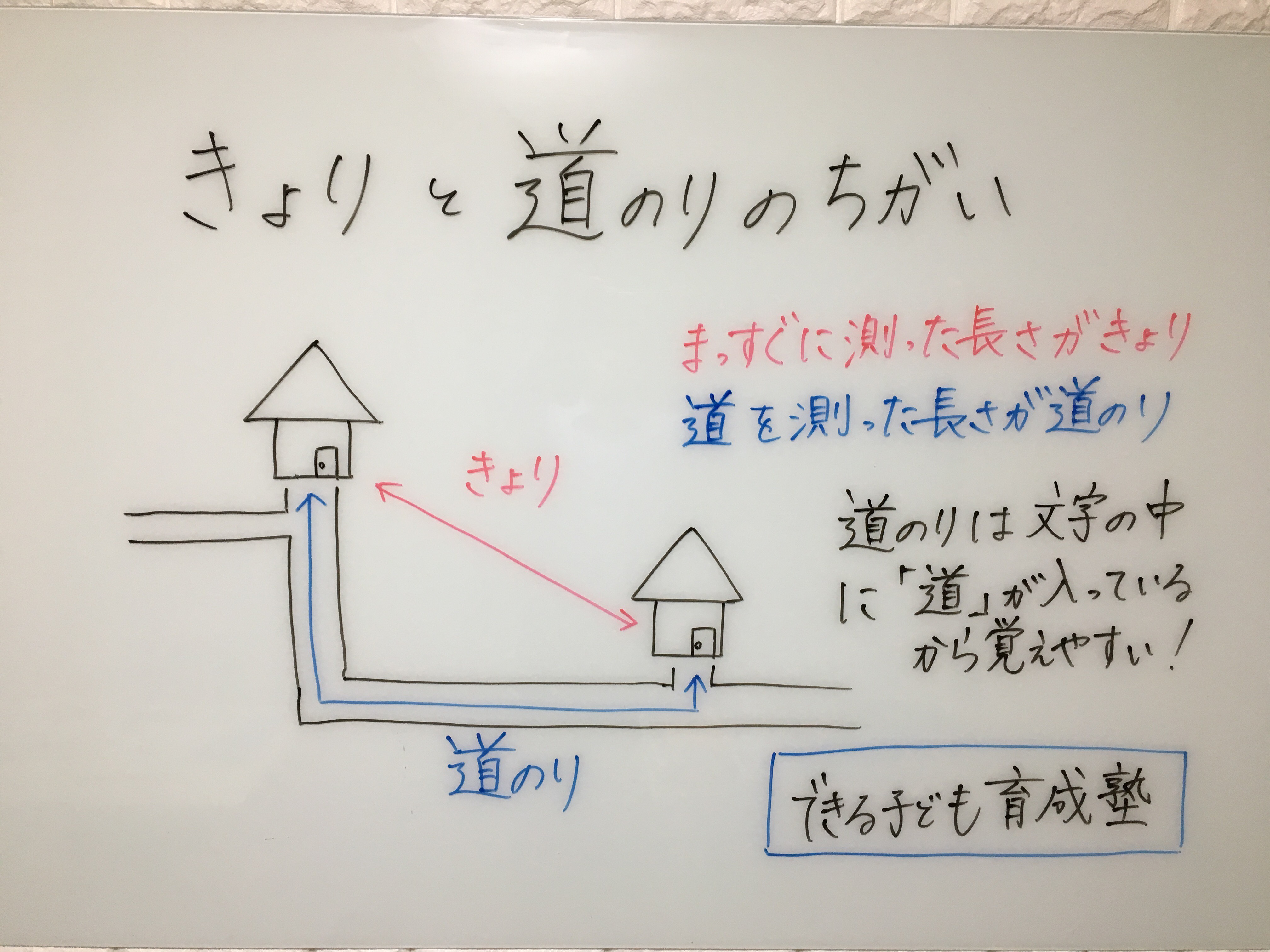



距離と道のりの違い 小学3年生の算数の問題 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




距離と道のり違いとは 小3算数に出てくる道のりの意味 Ruruのあれこれ日記




速さと時間から道のりを求める問題 家庭学習レシピ



キーワード 話し方カード 単元プラン を使った授業をしています 3年生算数 分数 New 中津市立真坂小学校



小学3年生の算数 の教え方の例 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月




すきるまドリル 小学3年生 算数 長いものの長さ 無料学習プリント すきるまドリル 無料学習プリント
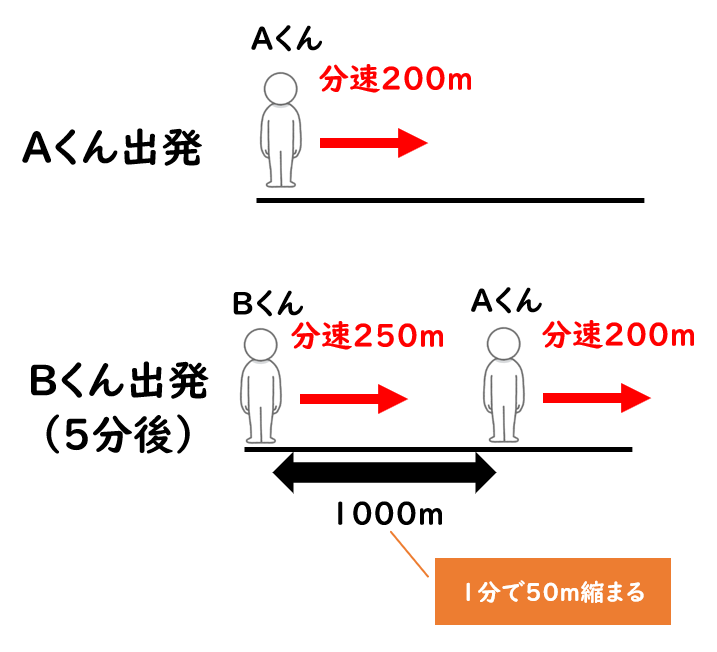



速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun
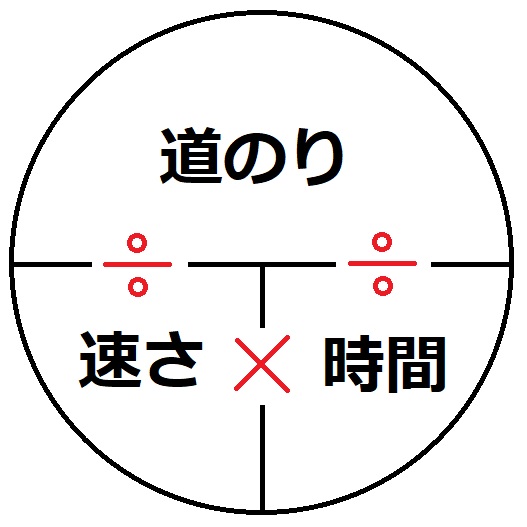



時速の計算が苦手なのは きはじ みはじ はじき に頼っているからだ ねんごたれログ




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




速さと単位 セルモ大蔵 世田谷 の塾長ブログ



5年算数速さ 教え方のポイント




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



小学3年生の算数 の教え方の例 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく



速さ 1 国際算数数学授業研究プロジェクト Impuls International Math Teacher Professionalization Using Lesson Study




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
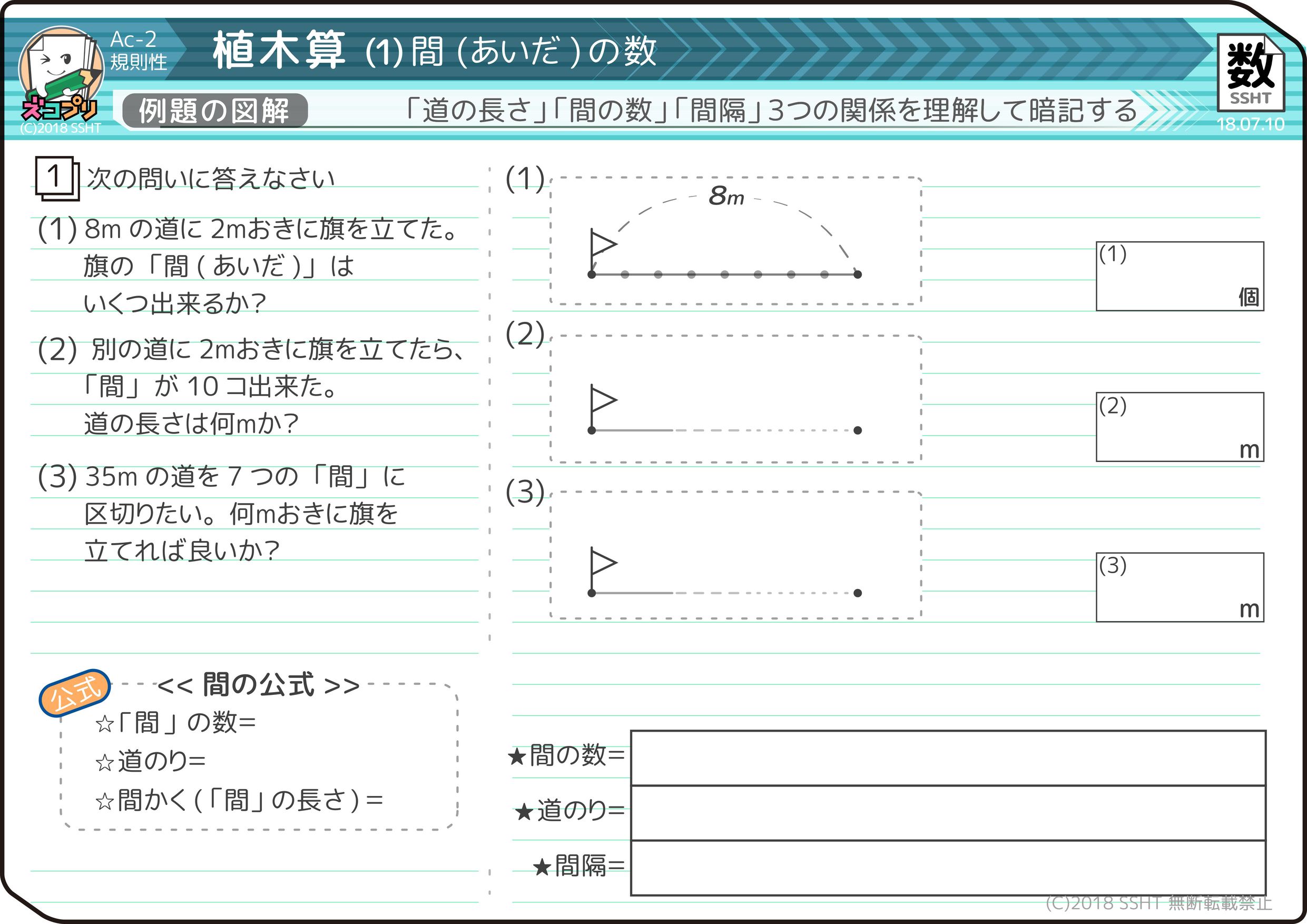



中学受験 植木算の教え方の2つのコツ 小学3年生にも分かりやすい そうちゃ式 受験算数 新1号館 数論 特殊算




きょりと道のりの練習問題 家庭学習レシピ




世界一分かりやすい算数 小6 速さ




すきるまドリル 小学6年生 算数 速さ 無料学習プリント すきるまドリル 無料学習プリント
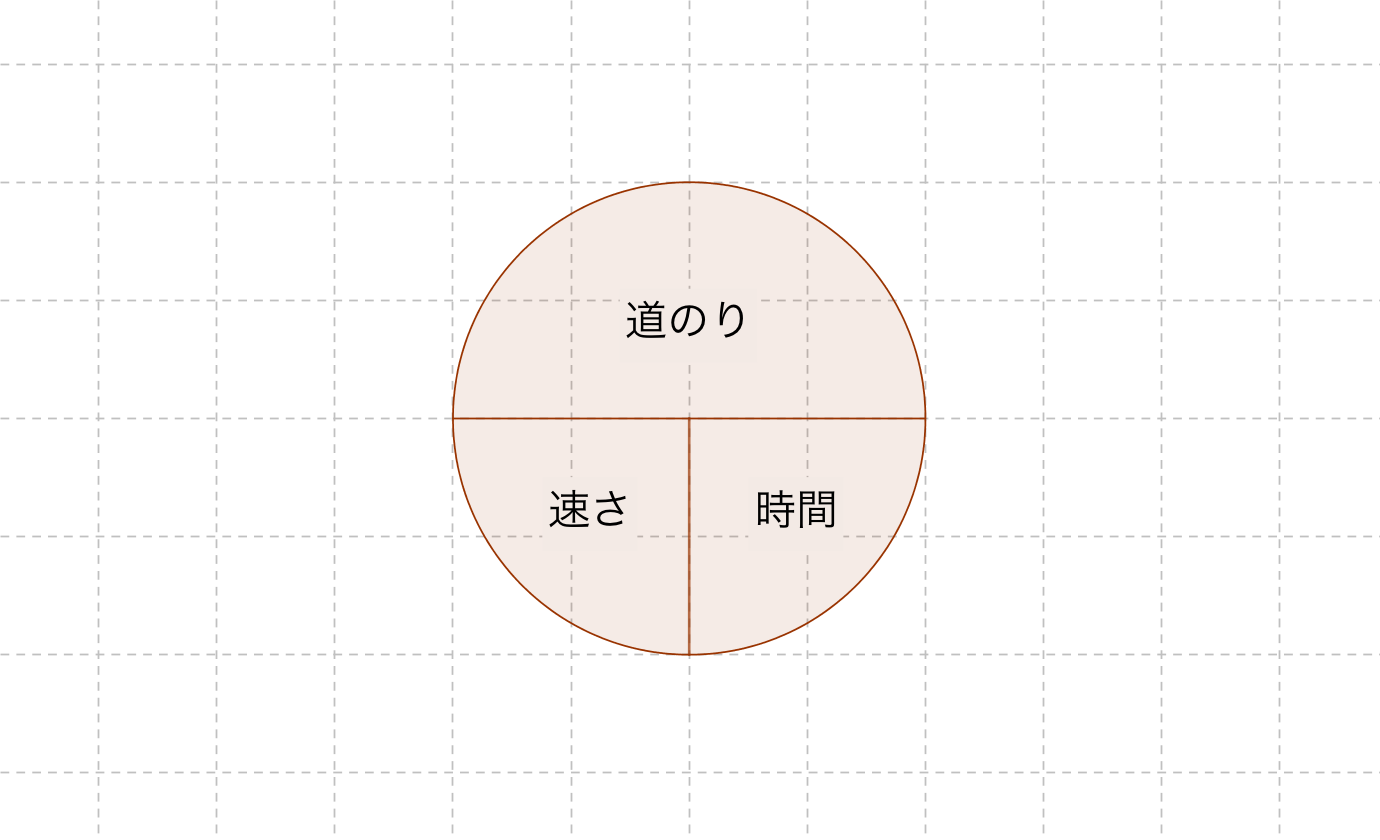



速さの公式 道のり 時間 算数の公式




距離と道のりの違い 小学3年生の算数の問題 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




小6 算数 小6 21 速さの表し方 基本編 Youtube




はじきの計算 例題を使って問題を解説 速さ 距離 時間を求める方法は 数スタ




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




世界一分かりやすい算数 小6 速さ
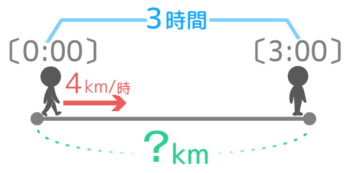



中学受験 速さの基本問題を分かりやすく図解 単位 三公式 ダイヤグラム そうちゃ式 受験算数 2号館 図形 速さ




きょりと道のりの練習問題 家庭学習レシピ




小6算数 速さ 時間 距離 道のり の文章題 ブログ アビット




往復の平均の速さ 間違えずに求められますか
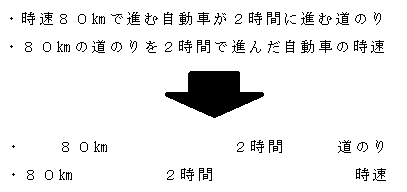



は じ き は悪魔の公式 算数が苦手な子には文章題はこう見えている 江南の塾 ネクサス 勉強のやり方専門塾 小中高一貫の少人数個別指導塾




小学5年生 算数 無料問題集 速さ 道のり 時間 おかわりドリル
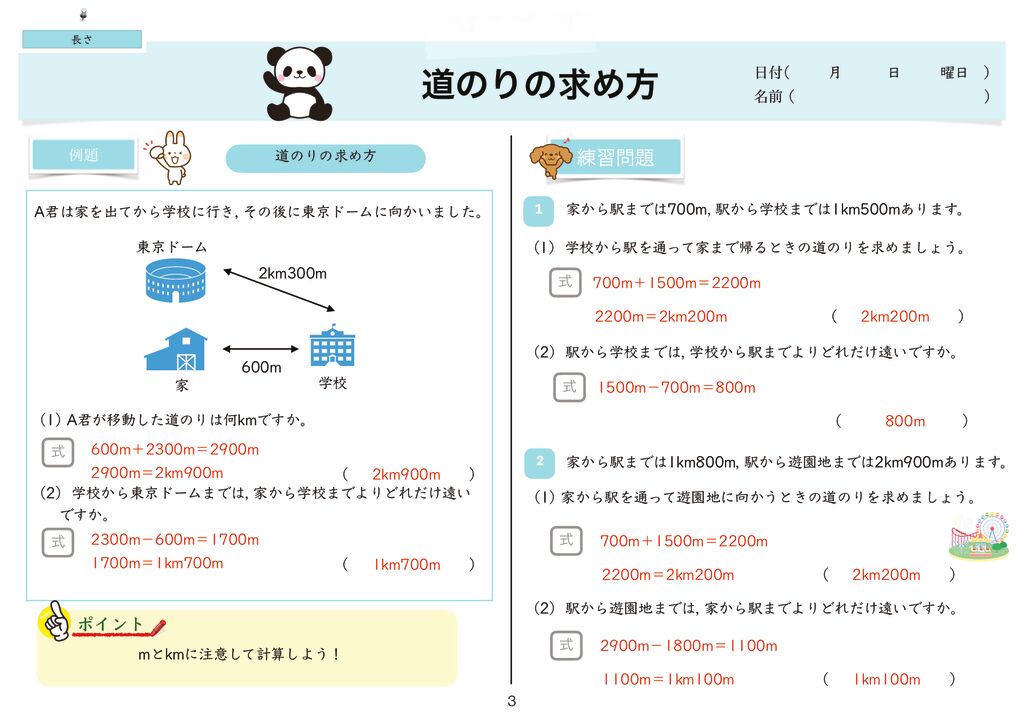



世界一分かりやすい算数 小3 長さ




速さや時間の単位が揃っていない道のりの求め方 みけねこ小学校
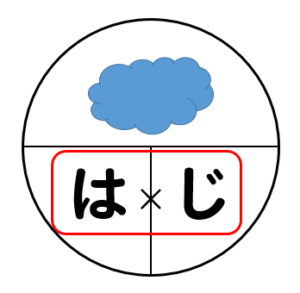



文字式 速さの問題をわかりやすく解く方法 数スタ
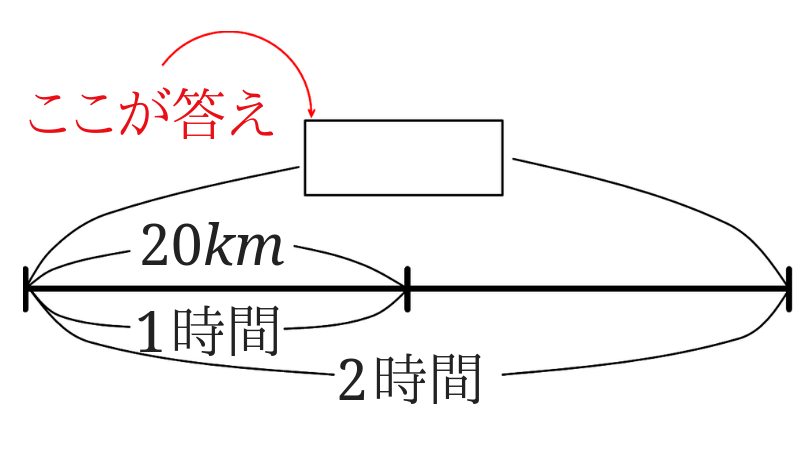



速さの公式に頼らない道のりの求め方ができるようになろう みけねこ小学校




速さ 時間 小6 分数で表されている時間の直し方 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




速さと時間から道のりを求める問題 家庭学習レシピ




中学受験 速さの基本問題を分かりやすく図解 単位 三公式 ダイヤグラム そうちゃ式 受験算数 2号館 図形 速さ



小学3年生の算数 の教え方の例 算数数学が苦手な子専門のプロ家庭教師みかん先生
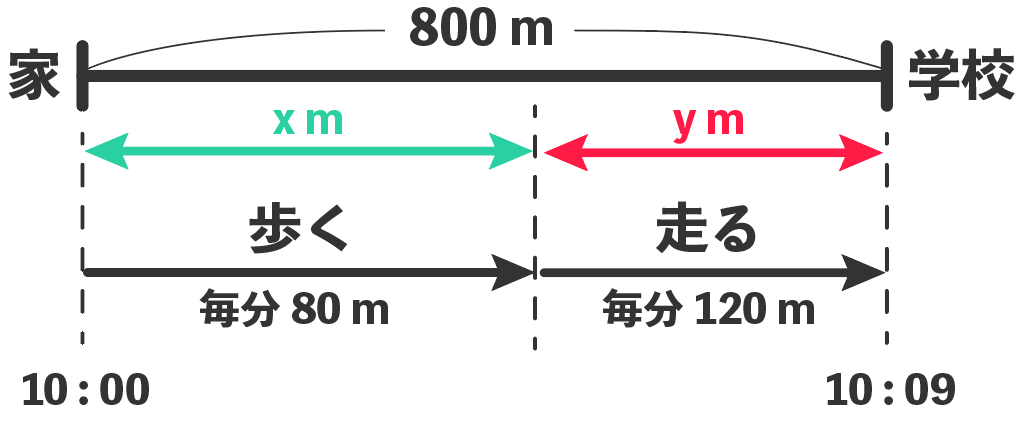



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく



5年算数速さ 教え方のポイント
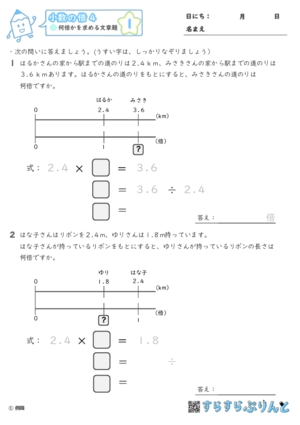



小数の倍とわり算 何倍かを求める文章題 小学5年生算数




仕事の原理などの単元で みはじ 道のり速さ時間 のような簡単に公式がわかる図 はない Clear



Www Nier Go Jp 21chousa Pdf 21seitourei Shou Sansuu Pdf




小3 算数 小3 31 長さをはかろう Youtube




小3 算数 小3 3 時こくと時間のもとめ方 Youtube
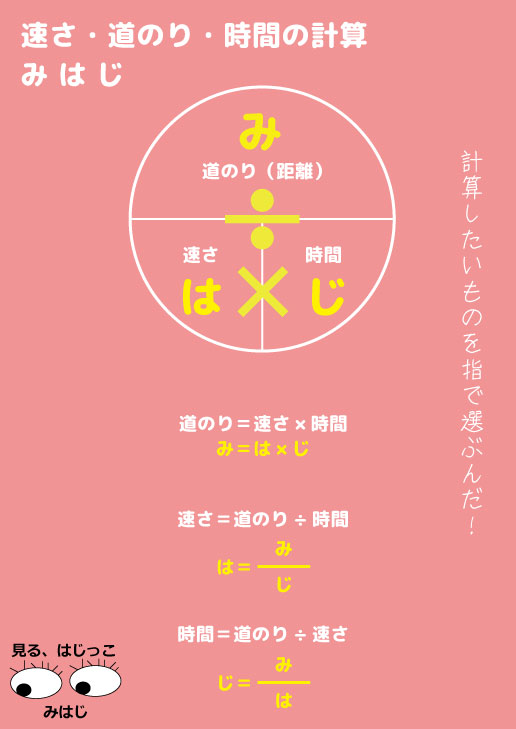



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい




世界一分かりやすい算数 小6 速さ



小学6年生の算数速さの問題でどうしても分かりません 計算の仕方教え Yahoo 知恵袋




道のりときょり 低学年の無料学習ドリル




19年度 1学期 3年生 ニューヨーク育英学園
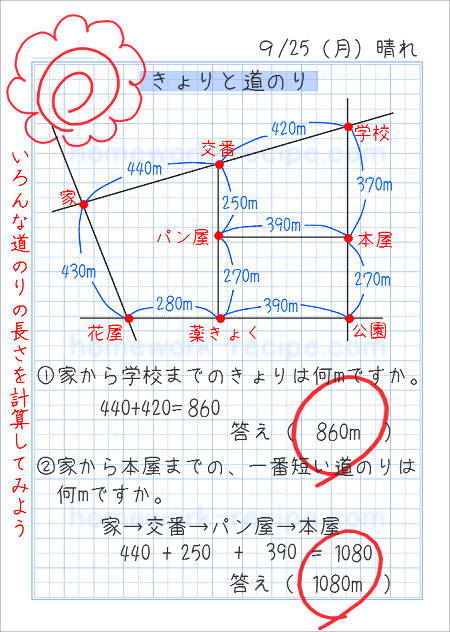



きょりと道のりの練習問題 家庭学習レシピ




ボード 教育 のピン




6年生算数ドリル 速さ




小学5年生 算数 無料問題集 速さ 道のり 時間 おかわりドリル



0 件のコメント:
コメントを投稿